E Xy E X E Y
Kalali
May 23, 2025 · 3 min read
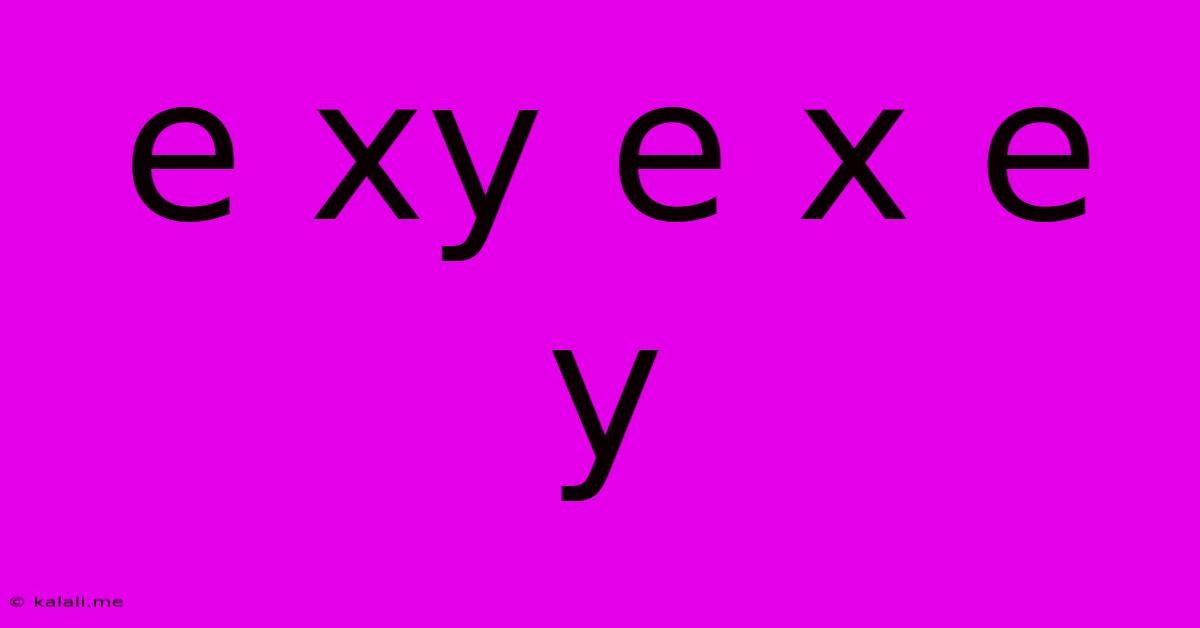
Table of Contents
Understanding the Mathematical Expression: e<sup>xy</sup>e<sup>x</sup>e<sup>y</sup>
This article explores the mathematical expression e<sup>xy</sup>e<sup>x</sup>e<sup>y</sup>, simplifying it and examining its properties. This seemingly complex expression can be significantly reduced using the fundamental rules of exponents. Understanding this simplification is key for anyone working with exponential functions in calculus, algebra, or related fields.
Simplifying the Expression
The core principle we'll leverage is the rule of combining exponents with the same base: a<sup>m</sup>a<sup>n</sup> = a<sup>m+n</sup>. Since all terms in our expression have the base e, we can apply this rule directly.
Let's break it down step-by-step:
-
Combining the first two terms: e<sup>xy</sup>e<sup>x</sup> can be rewritten as e<sup>xy + x</sup>. This is a direct application of the exponent rule mentioned above.
-
Combining the result with the third term: Now we have e<sup>xy + x</sup>e<sup>y</sup>. Applying the same rule again, we get e<sup>xy + x + y</sup>.
Therefore, the simplified form of e<sup>xy</sup>e<sup>x</sup>e<sup>y</sup> is e<sup>xy + x + y</sup>. This simplified expression is considerably more manageable and easier to work with in various mathematical contexts.
Applications and Further Exploration
This simplified expression, e<sup>xy + x + y</sup>, finds application in several areas:
-
Calculus: Derivatives and integrals involving exponential functions often require simplification before proceeding with calculations. This simplified form makes such calculations less cumbersome.
-
Differential Equations: Solutions to certain differential equations might involve expressions of this form, and simplification is crucial for understanding the solution's behavior.
-
Probability and Statistics: Exponential functions play a vital role in probability distributions like the exponential distribution and the normal distribution. Understanding how to simplify expressions like this can be valuable in these fields.
-
Physics and Engineering: Exponential functions frequently model growth and decay processes in physics and engineering. This simplified expression could represent aspects of these models.
Beyond Simplification: Exploring the Exponential Function
The exponential function, often represented as e<sup>x</sup>, is a fundamental function in mathematics with unique properties:
-
Always Positive: e<sup>x</sup> is always positive for any real number x.
-
Rapid Growth: The function exhibits rapid growth as x increases.
-
Inverse Function: Its inverse function is the natural logarithm, ln(x).
Understanding these properties is crucial for working with exponential expressions effectively.
Conclusion:
Simplifying the expression e<sup>xy</sup>e<sup>x</sup>e<sup>y</sup> to e<sup>xy + x + y</sup> is a straightforward application of fundamental exponent rules. This simplified form significantly aids in further mathematical manipulations and offers a clearer understanding of the expression's properties and applications across various scientific and mathematical disciplines. Remember, mastering the basic rules of exponents is paramount for success in advanced mathematics and related fields.
Latest Posts
Latest Posts
-
Why Does My Cat Follow Me To The Bathroom
May 23, 2025
-
Butter My Bottom And Call Me A Biscuit
May 23, 2025
-
Adobe Font Similar To League Spartan
May 23, 2025
-
Toilet Bowl Water Not Going Down
May 23, 2025
-
Six Legged Insect With Long Antennae
May 23, 2025
Related Post
Thank you for visiting our website which covers about E Xy E X E Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.