Equation For Circumference Of A Cylinder
Kalali
Mar 21, 2025 · 5 min read
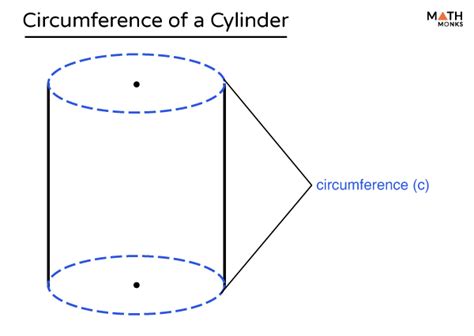
Table of Contents
The Equation for the Circumference of a Cylinder: A Deep Dive
The humble cylinder. A shape found everywhere from soda cans to tree trunks, its seemingly simple geometry hides a rich tapestry of mathematical concepts. While the term "circumference of a cylinder" might seem straightforward, understanding it thoroughly requires exploring related concepts like radius, diameter, and the crucial distinction between circumference and surface area. This comprehensive guide will unravel the equation, explore its applications, and delve into related geometrical calculations.
Understanding Cylindrical Geometry: Radius, Diameter, and Height
Before diving into the circumference equation itself, let's establish a firm foundation in the fundamental components of a cylinder:
-
Radius (r): The distance from the center of the circular base to any point on the circumference of that base. Think of it as half the diameter.
-
Diameter (d): The distance across the circular base, passing through the center. It's simply twice the radius (d = 2r).
-
Height (h): The perpendicular distance between the two circular bases of the cylinder. This is crucial for calculating surface area, but not directly relevant to circumference.
These three parameters—radius, diameter, and height—completely define the dimensions of any cylinder.
The Circumference Equation: It's All About the Circle
Crucially, the circumference of a cylinder refers to the circumference of its circular base (or top). A cylinder has two identical circular bases. Therefore, it doesn't have one circumference; rather, it has two identical circumferences.
The equation for the circumference (C) of a circle, and therefore the base of a cylinder, is:
C = 2πr
Where:
- C represents the circumference.
- π (pi): An irrational mathematical constant, approximately equal to 3.14159. It represents the ratio of a circle's circumference to its diameter.
- r represents the radius of the circular base.
Alternatively, using the diameter (d), the equation can be expressed as:
C = πd
Both equations are entirely equivalent; the choice depends on whether you know the radius or the diameter.
Practical Applications of the Circumference Equation
The circumference of a cylinder is crucial for a wide range of applications across various disciplines. Here are a few examples:
1. Engineering and Manufacturing:
-
Calculating Material Requirements: In manufacturing, determining the amount of material needed to construct a cylindrical component (like a pipe or a storage tank) relies heavily on knowing the circumference. This ensures the right amount of material is ordered, minimizing waste and maximizing efficiency.
-
Designing Machine Parts: The circumference dictates how components fit together. For example, designing a gear system requires precise calculations of circumference to ensure proper meshing and functionality.
-
Stress and Strain Analysis: In structural engineering, the circumference plays a vital role in calculations related to stress and strain on cylindrical structures under load.
2. Everyday Life:
-
Sizing Cylindrical Objects: From choosing the right-sized pipes for plumbing to selecting appropriate containers for storage, an understanding of circumference is essential.
-
Packaging and Labeling: The circumference is essential in determining the length of labels needed for cylindrical containers.
-
Calculating the Distance Around a Track: Imagine an athletics track designed as a cylinder (with straights and curves). The circumference of the curved section is crucial in calculating the total distance of a race.
Beyond Circumference: Surface Area and Volume
While circumference focuses on the perimeter of the circular base, the complete picture of a cylinder's geometry requires understanding its surface area and volume:
1. Lateral Surface Area:
The lateral surface area (A<sub>lateral</sub>) is the area of the curved surface of the cylinder, excluding the circular bases. The equation is:
A<sub>lateral</sub> = 2πrh
Where:
- r is the radius.
- h is the height.
2. Total Surface Area:
The total surface area (A<sub>total</sub>) includes both the lateral surface area and the areas of the two circular bases:
A<sub>total</sub> = 2πrh + 2πr²
This equation accounts for the entire surface of the cylinder.
3. Volume:
The volume (V) of a cylinder represents the space it occupies and is given by:
V = πr²h
This equation is fundamental in applications involving capacity, liquid storage, and material quantities.
Advanced Applications and Variations
The basic circumference equation forms the foundation for many more complex calculations. Let's explore a few examples:
-
Cylindrical Coordinates: In higher-level mathematics and physics, cylindrical coordinates (ρ, φ, z) are used to define points in three-dimensional space. The circumference is intrinsically linked to the ρ coordinate, representing the radial distance from the z-axis.
-
Curved Cylinders: The equations presented thus far apply to right circular cylinders (cylinders with straight, perpendicular sides). For cylinders with curved sides or non-circular bases, the calculations become significantly more complex, often requiring calculus and more advanced geometrical techniques.
-
Calculating Arc Length: If you need to find the length of only a portion of the circumference (an arc), you'll need to use a proportional calculation involving the angle subtended by that arc. The arc length (s) can be calculated using the formula: s = rθ, where θ is the angle in radians.
Practical Problems and Worked Examples
Let's solidify our understanding with some practical examples:
Problem 1: A cylindrical water tank has a radius of 2 meters. What is its circumference?
Solution: Using the equation C = 2πr, we have:
C = 2 * π * 2 meters = 4π meters ≈ 12.57 meters
Problem 2: A cylindrical pipe has a diameter of 10 centimeters. Calculate its circumference.
Solution: Using the equation C = πd, we have:
C = π * 10 cm = 10π cm ≈ 31.42 cm
Problem 3: A cylindrical can has a radius of 5 cm and a height of 15 cm. Calculate its total surface area.
Solution: Using the equation A<sub>total</sub> = 2πrh + 2πr², we have:
A<sub>total</sub> = 2π(5 cm)(15 cm) + 2π(5 cm)² = 150π cm² + 50π cm² = 200π cm² ≈ 628.32 cm²
Conclusion: Mastering Cylindrical Geometry
Understanding the equation for the circumference of a cylinder, along with its related concepts of surface area and volume, is fundamental to numerous fields. This guide has provided a comprehensive overview, covering the basic equations, practical applications, and extending to more complex scenarios. By mastering these calculations, you'll be well-equipped to tackle a wide range of geometrical problems and real-world applications involving cylindrical shapes. Remember to always clearly define the radius or diameter and choose the appropriate formula based on the given information. With practice, these concepts will become second nature, opening up a deeper appreciation for the fascinating world of geometry.
Latest Posts
Latest Posts
-
How Many Ounces Of Sour Cream Are In A Cup
Mar 28, 2025
-
Does A Catfish Have A Backbone
Mar 28, 2025
-
How Many Feet Are In 42 Inches
Mar 28, 2025
-
How Many Acres Is A Square Mile
Mar 28, 2025
-
15 Out Of 50 As A Percentage
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Equation For Circumference Of A Cylinder . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
