Equation Of Circle In Parametric Form
Kalali
Apr 05, 2025 · 6 min read
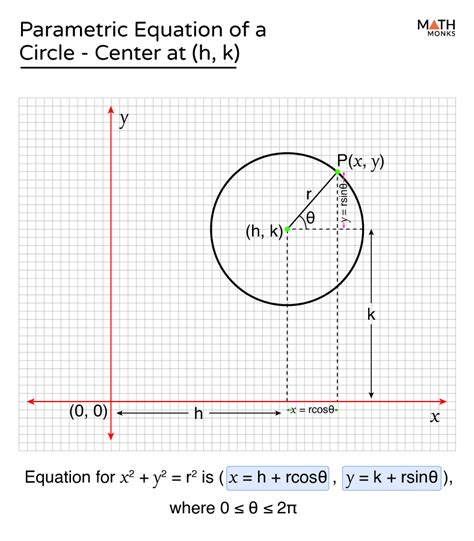
Table of Contents
The Equation of a Circle in Parametric Form: A Comprehensive Guide
The equation of a circle, a fundamental concept in geometry and mathematics, can be represented in various forms. While the standard Cartesian form (x-a)² + (y-b)² = r² is widely known, the parametric form offers a unique and powerful alternative, especially useful in various applications like animation, computer graphics, and physics simulations. This comprehensive guide will delve into the intricacies of the parametric equation of a circle, exploring its derivation, applications, and variations.
Understanding Parametric Equations
Before diving into the specifics of a circle, let's establish a foundational understanding of parametric equations. In essence, a parametric equation describes a curve or surface by expressing its coordinates as functions of a single parameter, often denoted as 't'. This parameter acts as an independent variable, and the coordinates (x, y) become dependent variables, defined by functions of 't'. This approach contrasts with the implicit or explicit forms where one coordinate is directly expressed as a function of the other.
For example, consider the parametric equations x = t and y = t². This represents a parabola. As 't' varies, the (x, y) coordinates trace out the parabola's path. The power of parametric equations lies in their ability to describe complex curves using simple functions of 't'.
Deriving the Parametric Equation of a Circle
Let's derive the parametric equation of a circle centered at the origin (0, 0) with radius 'r'. We can leverage the trigonometric functions sine and cosine to accomplish this. Consider a point (x, y) on the circle. The angle 't' that the line segment connecting the origin to (x, y) makes with the positive x-axis can be our parameter.
From basic trigonometry, we know:
- x = r * cos(t)
- y = r * sin(t)
These are the parametric equations of a circle centered at the origin. As 't' varies from 0 to 2π (or 0 to 360 degrees), the point (x, y) traces the entire circumference of the circle. The parameter 't' represents the angle swept out from the positive x-axis.
Visualizing the Parameter 't': Imagine a line segment rotating counter-clockwise around the origin. The angle this line segment makes with the positive x-axis at any instant is 't'. The endpoint of this line segment, which lies on the circle, has coordinates (x, y) defined by the parametric equations.
Shifting the Center: Parametric Equation of a Circle with an Arbitrary Center
The equations above are for a circle centered at the origin. To shift the center to an arbitrary point (a, b), we simply translate the coordinates:
- x = a + r * cos(t)
- y = b + r * sin(t)
This is the general parametric equation of a circle with center (a, b) and radius r. These equations provide a complete and versatile description of any circle in the Cartesian plane.
Applications of the Parametric Equation of a Circle
The parametric form of a circle offers several advantages over the standard Cartesian form, making it particularly useful in various applications:
1. Computer Graphics and Animation:
Generating smooth, continuous circular motion in computer graphics and animation is effortlessly achieved using parametric equations. By incrementally increasing the value of 't', we can easily calculate successive points on the circle, creating the illusion of motion. This method avoids the complexities of directly solving for y in terms of x, which is needed when using the implicit Cartesian form.
2. Physics Simulations:
Many physical phenomena involve circular motion, such as planetary orbits, rotational mechanics, and oscillatory systems. Parametric equations provide a natural and efficient way to model these systems. For example, simulating projectile motion with air resistance often leverages parametric equations to model the trajectory.
3. Calculus and Vector Calculus:
Parametric equations simplify the calculation of tangent lines, arc length, and other geometric properties of the circle. Determining the tangent vector at any point on the curve is straightforward using derivatives with respect to 't'. This simplifies calculations compared to implicit differentiation in the Cartesian form.
4. Engineering and Design:
Circular elements are fundamental in numerous engineering applications, ranging from gear design and cam mechanisms to the design of pipelines and pressure vessels. Using parametric equations, engineers can model these circular components efficiently and precisely.
Variations and Extensions
The basic parametric equations can be extended and modified to represent various related geometric concepts:
1. Clockwise Rotation:
The equations presented earlier describe counter-clockwise rotation. To achieve clockwise rotation, simply replace 't' with '-t':
- x = a + r * cos(-t)
- y = b + r * sin(-t)
Remembering that cos(-t) = cos(t) and sin(-t) = -sin(t), this can be simplified to:
- x = a + r * cos(t)
- y = b - r * sin(t)
2. Partial Circles (Arcs):
Instead of tracing the full circle, we can generate specific arcs by restricting the range of 't'. For instance:
- To generate the upper semicircle, let 't' vary from 0 to π.
- To generate the right semicircle, let 't' vary from -π/2 to π/2.
By adjusting the range of 't', any portion of the circle can be generated.
3. Ellipses:
The parametric equation can be extended to represent ellipses. An ellipse centered at (a, b) with semi-major axis 'r1' and semi-minor axis 'r2' is given by:
- x = a + r1 * cos(t)
- y = b + r2 * sin(t)
This simple modification expands the application of parametric representations to a broader class of curves.
Comparing Parametric and Cartesian Forms
Both parametric and Cartesian forms have their strengths and weaknesses:
Cartesian Form ( (x-a)² + (y-b)² = r² ):
- Advantages: Compact, easy to visualize the circle's properties (center and radius). Simple to determine if a point lies on the circle.
- Disadvantages: Less convenient for generating points along the circle's circumference, particularly for dynamic applications. More complex for certain calculus operations (like finding tangents).
Parametric Form ( x = a + r * cos(t), y = b + r * sin(t) ):
- Advantages: Excellent for generating points along the circle, ideal for animation and simulations. Simplifies many calculus operations.
- Disadvantages: Slightly more complex notation than the Cartesian form. Requires understanding of parametric equations.
Conclusion
The parametric equation of a circle provides a powerful and versatile alternative to the standard Cartesian representation. Its elegance and adaptability make it a crucial tool in diverse fields, from computer graphics and animation to physics simulations and engineering design. Understanding and applying this form enhances one's capabilities in representing and manipulating circular geometry effectively. The flexibility of adjusting the parameters allows for the generation of partial circles, ellipses, and the control of rotation direction, making this a truly indispensable concept in mathematical modeling and graphical representation. By mastering the parametric form, one unlocks a deeper understanding of the circle and its applications.
Latest Posts
Latest Posts
-
7am To 11am Is How Many Hours
Jul 12, 2025
-
If Your 35 What Year Was You Born
Jul 12, 2025
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
-
30 X 30 Is How Many Square Feet
Jul 12, 2025
-
How Much Does A Half Oz Weigh
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about Equation Of Circle In Parametric Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.