Expand And Simplify X 5 X 4
Kalali
Jun 11, 2025 · 2 min read
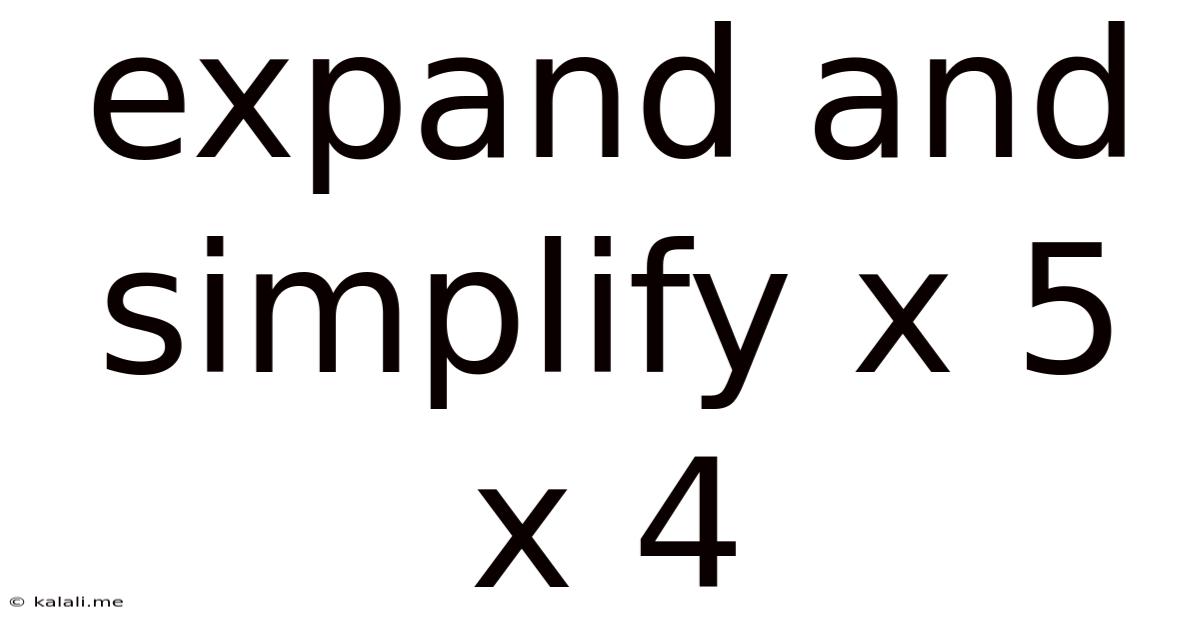
Table of Contents
Expanding and Simplifying x 5 x 4: A Step-by-Step Guide
Meta Description: Learn how to expand and simplify the algebraic expression x * 5 * 4 easily. This guide provides a step-by-step explanation perfect for beginners in algebra. We'll cover the order of operations and the concept of simplification to help you master this fundamental algebraic skill.
Expanding and simplifying algebraic expressions is a fundamental skill in mathematics, particularly in algebra. This guide will walk you through the process of expanding and simplifying the expression x * 5 * 4. While seemingly simple, understanding this process lays the groundwork for tackling more complex algebraic manipulations.
Understanding the Expression
The expression x * 5 * 4 represents multiplication of three terms: a variable 'x', and the constants 5 and 4. The asterisk (*) symbol denotes multiplication. Our goal is to write this expression in a simpler, more concise form.
The Commutative Property of Multiplication
Multiplication possesses a crucial property called the commutative property. This means that the order of the numbers being multiplied does not affect the result. Therefore, x * 5 * 4 is equivalent to x * 4 * 5, 5 * x * 4, and so on. This flexibility allows us to rearrange the terms for easier simplification.
Step-by-Step Simplification
-
Combine the constants: We can multiply the constants 5 and 4 together first. 5 * 4 = 20.
-
Rewrite the expression: This leaves us with x * 20.
-
Simplified form: The simplified form of the expression x * 5 * 4 is 20x.
Therefore, expanding and simplifying x * 5 * 4 results in the equivalent expression 20x. This simplified form is often preferred in algebra as it's more compact and easier to work with in further calculations or equation solving.
Practical Application and Further Exploration
This seemingly basic example forms the foundation for more advanced algebraic manipulations. Understanding how to simplify expressions like this is crucial for solving equations, simplifying complex formulas, and ultimately, mastering more advanced mathematical concepts. Remember to always follow the order of operations (PEMDAS/BODMAS) when dealing with expressions involving multiple operations.
This exercise highlights the importance of understanding the commutative property and the ability to group and simplify numerical components to efficiently represent algebraic expressions. By mastering these basic principles, you'll build a strong foundation for more advanced algebraic work.
Latest Posts
Latest Posts
-
How Many Guppies In A 5 Gallon Tank
Jul 01, 2025
-
How To Beat Stage 7 In Bloxorz
Jul 01, 2025
-
How Much Oz In A Bottle Of Water
Jul 01, 2025
-
How Long Does It Take To Drive 10 Miles
Jul 01, 2025
-
How Many 9s Are In A Deck Of Cards
Jul 01, 2025
Related Post
Thank you for visiting our website which covers about Expand And Simplify X 5 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.