Exterior Angles Of A Circle Theorem
Kalali
Apr 05, 2025 · 6 min read
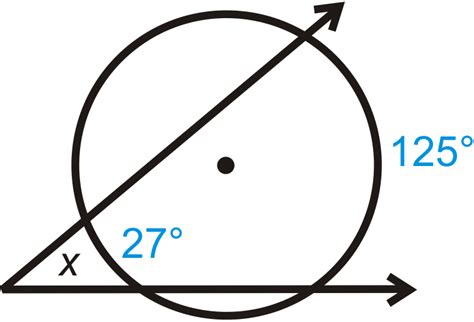
Table of Contents
Exterior Angles of a Circle Theorem: A Comprehensive Guide
The exterior angle of a circle theorem, while seemingly simple at first glance, holds a significant place in geometry and possesses surprising depth and applicability. This comprehensive guide will explore this theorem in detail, unraveling its nuances, providing multiple proofs, and demonstrating its utility in solving various geometric problems. We’ll delve into its connection to other circle theorems, explore practical applications, and offer exercises to solidify your understanding.
Understanding the Theorem
The exterior angle of a circle theorem states: The angle between a tangent and a chord drawn from the point of contact is equal to the angle in the alternate segment.
Let's break this down:
- Tangent: A straight line that touches a circle at exactly one point.
- Chord: A straight line segment whose endpoints both lie on the circle.
- Point of Contact: The single point where the tangent touches the circle.
- Alternate Segment: The segment of the circle that is opposite the angle formed by the tangent and chord.
Visual Representation:
Imagine a circle with a tangent line touching it at point T. From point T, draw a chord, creating an angle between the tangent and the chord. Now, consider the arc of the circle on the opposite side of the chord from this angle. The angles subtended by this arc within the segment are all equal to the angle formed by the tangent and chord.
This theorem provides a powerful relationship between angles formed by tangents, chords, and the arcs they subtend within a circle.
Proof of the Theorem
There are several ways to prove the exterior angle theorem. Here are two common approaches:
Proof 1: Using Similar Triangles
-
Construction: Draw a line from the point where the chord meets the circle (let's call this point A) to a point on the circle in the alternate segment (let's call this point B). Extend this line until it intersects the tangent.
-
Angle Properties: Observe that the angles subtended by the same arc (the arc between A and B) are equal. This establishes the equality of one pair of angles.
-
Similar Triangles: By using alternate interior angles and angle properties formed by a tangent and chord, it can be shown that two triangles formed (one with the tangent and chord, and another involving the chord and a point in the alternate segment) are similar.
-
Ratio of Sides: Because the triangles are similar, the ratios of corresponding sides are equal. Through careful manipulation of this ratio, we can show the equality of the angle formed by the tangent and chord and the angle in the alternate segment.
Proof 2: Using the Angle in a Semicircle Theorem
-
Construction: Draw a diameter from the point of contact of the tangent.
-
Angle in a Semicircle: The angle subtended by the diameter at any point on the circle is a right angle (90 degrees).
-
Angle Sum of a Triangle: Utilize the angle sum property of triangles to express the angle formed by the tangent and chord in terms of angles in the relevant triangle.
-
Deduction: By carefully manipulating angle relationships and applying the angle in a semicircle theorem, the equality between the angle formed by the tangent and chord and the angle in the alternate segment can be deduced.
Applications of the Theorem
The exterior angle of a circle theorem isn't just a theoretical concept; it finds significant practical applications in various areas:
-
Solving Geometric Problems: The theorem allows us to find unknown angles in circles given specific information about tangents and chords. This is crucial in areas like surveying, architecture, and engineering, where accurate angle measurements are essential.
-
Calculating Arc Lengths and Segment Areas: By understanding the relationship between angles and arcs, the theorem enables us to indirectly calculate the length of arcs and the area of segments within a circle.
-
Proofs of Other Theorems: The theorem serves as a cornerstone in proving other important geometrical theorems related to circles. Its understanding is vital for developing a comprehensive understanding of circle geometry.
-
Computer Graphics and Animation: The principles of circle geometry, including this theorem, are fundamental in computer graphics and animation for creating realistic curves and circular movements in digital designs.
-
Engineering and Design: Precise angle calculations are crucial in several engineering disciplines, such as designing gears, cams, and other circular mechanisms. This theorem helps in such precise calculations.
Connecting the Theorem to Other Circle Theorems
The exterior angle of a circle theorem is intimately connected to several other key circle theorems:
-
Angle at the Center Theorem: This theorem establishes the relationship between the angle subtended by an arc at the center of the circle and the angle subtended by the same arc at the circumference. Understanding this theorem is critical for understanding the exterior angle theorem's relationship to the arc in the alternate segment.
-
Angle in a Semicircle Theorem: As illustrated in one of the proofs above, this theorem (which states that the angle subtended by a diameter in a semicircle is always 90 degrees) plays a significant role in demonstrating the validity of the exterior angle theorem.
-
Cyclic Quadrilateral Theorem: While seemingly unrelated at first, the exterior angle theorem can be used to prove properties of cyclic quadrilaterals (quadrilaterals whose vertices lie on a circle).
Example Problems
Let's illustrate the practical application of the exterior angle theorem with a few examples:
Example 1:
A tangent touches a circle at point A. A chord AB is drawn from A. The angle between the tangent and chord AB is 35 degrees. What is the angle subtended by the arc AB in the alternate segment?
Solution: According to the exterior angle theorem, the angle in the alternate segment is equal to the angle between the tangent and chord. Therefore, the angle in the alternate segment is 35 degrees.
Example 2:
A circle has a tangent touching it at point P. A chord PQ is drawn, forming an angle of 40 degrees between the tangent and the chord. Another chord PR is drawn, forming an angle of x degrees with the tangent. If the angles subtended by arc QR in the alternate segments are both equal to y degrees, what is the value of x and y?
Solution: The angle between the tangent and chord PQ (40 degrees) is equal to the angle subtended by arc PQ in the alternate segment. Similarly, the angle between the tangent and chord PR (x degrees) is equal to the angle subtended by arc PR in the alternate segment. Since angles in the same segment are equal, y = 40 degrees and x = y = 40 degrees.
Example 3: (More challenging)
In a circle, a tangent at point A intersects a secant at point B. The secant intersects the circle at points C and D. If angle BAC is 25 degrees and angle BCA is 70 degrees, find angle CAD.
Solution: This problem requires the application of several circle theorems, including the exterior angle theorem. Using the properties of triangles and the exterior angle theorem, you can find the value of angle CAD.
Conclusion
The exterior angle of a circle theorem is a fundamental concept in geometry with broad applications. Understanding this theorem and its interconnections with other circle theorems is vital for solving a variety of geometric problems. By mastering this theorem, you’ll gain a deeper appreciation of circle geometry and its importance in many fields. This comprehensive guide provided multiple proofs, practical applications, and examples, equipping you with the knowledge to confidently tackle challenges involving this significant theorem. Remember to practice solving various problems to solidify your understanding and build your problem-solving skills. The more you work with this theorem, the more intuitively you'll grasp its power and utility.
Latest Posts
Latest Posts
-
How Many Ml In 5 L
Apr 05, 2025
-
What Is 1 8 Oz In Grams
Apr 05, 2025
-
180 Ml Is How Many Cups
Apr 05, 2025
-
What Is 9 As A Fraction
Apr 05, 2025
-
How Many Quarts In 8 Cups
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Exterior Angles Of A Circle Theorem . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
