F X Y X 2 Y 2
Kalali
Jun 04, 2025 · 3 min read
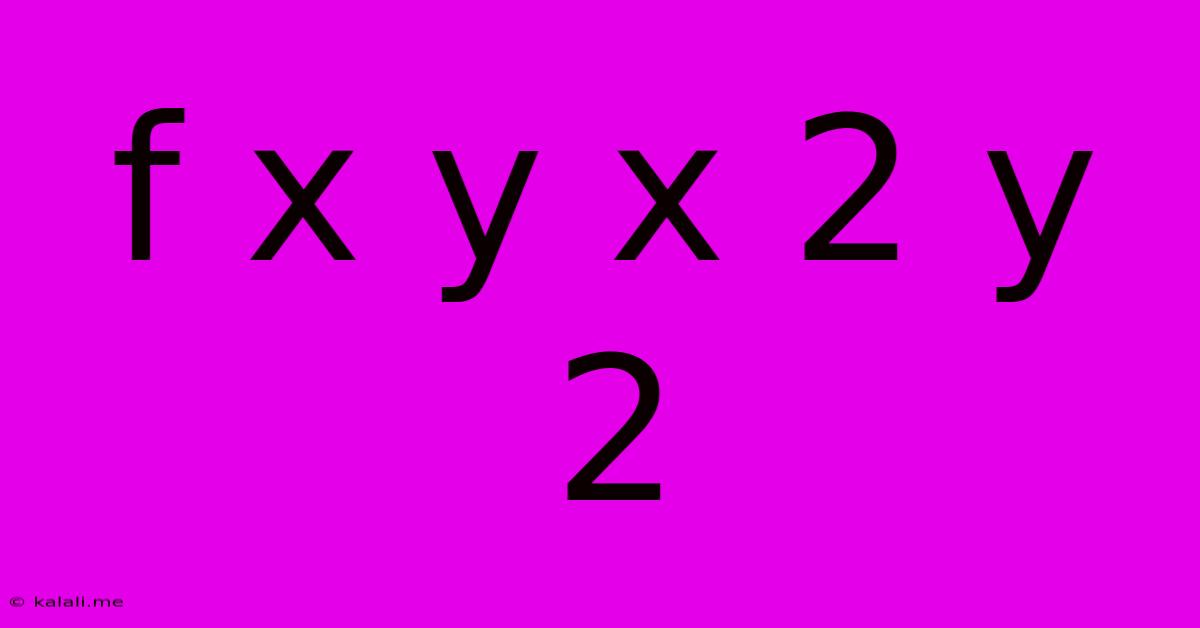
Table of Contents
Exploring the Mathematical Expression: f(x, y) = x² + y²
This article delves into the mathematical expression f(x, y) = x² + y², exploring its properties, graphical representation, and applications. Understanding this seemingly simple function reveals fundamental concepts in mathematics and its various applications across different fields.
What does f(x, y) = x² + y² represent?
The expression f(x, y) = x² + y² represents a function of two variables, x and y. For every pair of input values (x, y), the function outputs a single value, calculated by squaring x, squaring y, and then adding the results. This function is a fundamental example in multivariable calculus and has significant geometric interpretations. It's also closely related to the concept of distance from the origin in a two-dimensional coordinate system.
Geometric Interpretation: The Circular Surface
The most insightful way to understand this function is through its graphical representation. Plotting this function in three-dimensional space (where z = f(x, y)) results in a paraboloid, a three-dimensional surface that resembles a bowl or a satellite dish. The paraboloid opens upwards, and the value of z increases as you move away from the origin (0, 0). Cross-sections of this paraboloid parallel to the xy-plane (for constant z values) are circles. This shows a direct relationship to the distance formula, which we'll explore further.
Connection to the Distance Formula
The equation x² + y² = r² represents a circle with radius 'r' centered at the origin in a two-dimensional plane. The function f(x, y) = x² + y² can be interpreted as the square of the distance from any point (x, y) to the origin (0, 0). The square root of f(x, y), √(x² + y²), gives the actual Euclidean distance. This connection is crucial in various applications, including physics, engineering, and computer graphics.
Applications and Further Exploration
The seemingly simple function f(x, y) = x² + y² has a wide range of applications:
- Distance Calculations: As mentioned earlier, it's fundamental in calculating distances in two-dimensional space. This has implications in navigation, mapping, and various other fields.
- Optimization Problems: Finding minimum or maximum values of this function (or functions derived from it) is a common problem in optimization.
- Signal Processing: The function is used in signal processing and image analysis. It's often a building block for more complex algorithms.
- Physics: This function appears in various physics formulas related to potential energy, particularly in systems with radial symmetry.
- Computer Graphics: It plays a vital role in rendering and manipulating graphics.
Variations and Extensions
We can extend this concept to three or more dimensions. For instance, in three dimensions, the function f(x, y, z) = x² + y² + z² represents the square of the distance from a point (x, y, z) to the origin, and its graphical representation would be a paraboloid in four dimensions. This highlights the scalability and adaptability of the core concept.
In conclusion, the seemingly simple function f(x, y) = x² + y² holds significant mathematical importance and numerous applications across diverse fields. Understanding its geometric interpretation and its connection to distance calculations provides a solid foundation for exploring more complex mathematical concepts and their practical implications.
Latest Posts
Latest Posts
-
How To Connect 10 3 Wire To A 30 Amp Breaker
Jun 06, 2025
-
Why Did God Create A Man
Jun 06, 2025
-
How Hot Can A Wood Fire Get
Jun 06, 2025
-
Symptoms Of Bad Thermostat On Hot Water Heater
Jun 06, 2025
-
Is It Legal To Make A Horcrux In Harry Potter
Jun 06, 2025
Related Post
Thank you for visiting our website which covers about F X Y X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.