Find The Domain Of The Graphed Function Apex
Kalali
Mar 30, 2025 · 6 min read
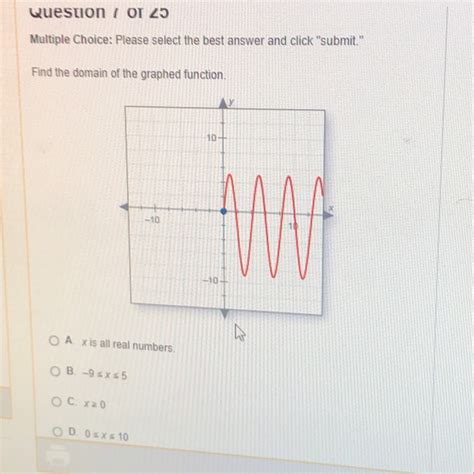
Table of Contents
Decoding the Domain of Graphed Functions: A Comprehensive Guide
Finding the domain of a graphed function might seem daunting at first, but with a structured approach and a clear understanding of core concepts, it becomes a manageable and even enjoyable task. This comprehensive guide will equip you with the knowledge and techniques to confidently determine the domain of any graphed function, effectively navigating the complexities of function analysis.
Understanding the Domain: The Foundation
Before delving into specific examples, let's solidify our understanding of the domain itself. The domain of a function refers to the set of all possible input values (often represented by x) for which the function is defined. In simpler terms, it's the range of x-values where the function exists and produces a valid output (y-value). Conversely, values excluded from the domain are those that would lead to undefined results, such as division by zero or the square root of a negative number.
Identifying the domain from a graph is a visual process. We look for the x-values covered by the graph. Any gaps or breaks in the graph indicate values not included in the domain.
Visual Inspection Techniques: Deciphering the Graph
Analyzing the graph is the most direct method to determine the domain. Here are some key visual cues and corresponding interpretations:
1. Continuous Graphs:
If the graph is a continuous line or curve with no breaks or interruptions, its domain typically spans across all real numbers. We represent this using interval notation as (-∞, ∞) or using set-builder notation as {x | x ∈ ℝ}. This means the function is defined for every possible real number x.
2. Discontinuous Graphs with Breaks:
Graphs with breaks or discontinuities require careful attention. The domain excludes the x-values corresponding to these breaks.
- Jump Discontinuities: These are sudden jumps in the graph's value. The domain excludes the x-value where the jump occurs.
- Removable Discontinuities (Holes): These appear as holes in the graph, indicating a specific x-value where the function is undefined but could potentially be defined with a slight adjustment. The domain still excludes this x-value.
- Infinite Discontinuities (Asymptotes): These occur when the function approaches infinity or negative infinity as x approaches a specific value. This specific x-value is excluded from the domain. Vertical asymptotes are particularly indicative of values excluded from the domain.
3. Graphs with Endpoints:
Graphs that have clear endpoints – meaning the graph stops at specific x-values – have domains limited by these endpoints. These endpoints can be included (closed circle) or excluded (open circle) depending on whether the function is defined at the endpoint or not.
- Closed Endpoint (Included): If the endpoint is represented by a closed circle (•), the corresponding x-value is included in the domain.
- Open Endpoint (Excluded): If the endpoint is represented by an open circle (◦), the corresponding x-value is excluded from the domain.
4. Piecewise Functions:
Piecewise functions are defined by different expressions over different intervals. The domain is the union of all intervals where the individual pieces are defined. Carefully examine each piece to identify its domain, then combine them to get the overall domain.
Interval Notation and Set-Builder Notation: Expressing the Domain
Once you've visually identified the domain, you'll need to express it formally using either interval notation or set-builder notation. Let's explore both methods:
1. Interval Notation: This method uses parentheses and brackets to indicate whether endpoints are included or excluded:
- Parentheses ( ): Used for open intervals, indicating that the endpoint is not included.
- Brackets [ ]: Used for closed intervals, indicating that the endpoint is included.
- Infinity (∞) and Negative Infinity (-∞): Always used with parentheses, as infinity is not a number.
Example: If the domain spans from x = 2 (included) to x = 7 (excluded), the interval notation is [2, 7).
2. Set-Builder Notation: This method uses set notation to define the domain:
- { x | condition }: This reads "the set of all x such that the condition is true."
- The condition specifies the restrictions on the x-values.
Example: For the same domain as above, the set-builder notation is {x | 2 ≤ x < 7}.
Practical Examples: Analyzing Different Graph Types
Let's solidify these concepts with some practical examples of different graph types:
Example 1: A Simple Linear Function
Imagine a straight line extending infinitely in both directions. This represents a continuous function defined for all real numbers. The domain is therefore (-∞, ∞) or {x | x ∈ ℝ}.
Example 2: A Parabola
A parabola, whether opening upwards or downwards, typically extends infinitely to the left and right. Again, its domain is usually (-∞, ∞) or {x | x ∈ ℝ}. However, a parabola defined by a piecewise function could have a limited domain.
Example 3: A Rational Function with a Vertical Asymptote
Consider a rational function with a vertical asymptote at x = 3. This means the function is undefined at x = 3. The domain would be (-∞, 3) ∪ (3, ∞) or {x | x ≠ 3}. The union symbol (∪) indicates that the domain is the combination of two separate intervals.
Example 4: A Square Root Function
The square root function, √x, is only defined for non-negative values of x. Therefore, its domain is [0, ∞) or {x | x ≥ 0}.
Example 5: A Piecewise Function
Consider a piecewise function defined as:
f(x) = x² for x ≤ 1 f(x) = x + 1 for x > 1
The first piece, x², is defined for all real numbers less than or equal to 1. The second piece, x + 1, is defined for all real numbers greater than 1. Combining these, the domain of the entire piecewise function is (-∞, ∞) or {x | x ∈ ℝ}.
Example 6: A Function with a Hole
Imagine a graph that looks like a straight line but has a single "hole" at x = 2. This indicates a removable discontinuity. The domain is (-∞, 2) ∪ (2, ∞) or {x | x ≠ 2}.
Advanced Considerations: Implicit Functions and More Complex Scenarios
While the visual inspection method works well for many functions, some scenarios demand a more analytical approach:
- Implicit Functions: Functions defined implicitly (e.g., x² + y² = 1) require solving for y to express the function explicitly before determining the domain.
- Trigonometric Functions: The domains of trigonometric functions (sin x, cos x, tan x, etc.) are cyclical and require careful consideration of their periodic nature.
- Logarithmic Functions: Logarithmic functions (logₐ x) are only defined for positive values of x (x > 0) and where the base 'a' is greater than zero and not equal to 1.
- Functions involving other restricted operations: This includes absolute values, inverse trigonometric functions, and any functions with restrictions on their input values.
For these more complex cases, understanding the inherent restrictions of each function type is crucial. Consulting relevant mathematical resources and applying algebraic manipulation techniques will often prove essential.
Conclusion: Mastering Domain Determination
Determining the domain of a graphed function is a fundamental skill in function analysis. By combining visual inspection with a strong understanding of interval and set-builder notation, and by considering potential restrictions based on function type, you can confidently navigate even the most complex graphs and accurately define their domains. Remember to always carefully consider the visual cues of the graph, paying close attention to breaks, asymptotes, and endpoints. Practice is key—the more you work with different graph types and functions, the more intuitive this process will become.
Latest Posts
Latest Posts
-
In What Episode Of Bleach Does Ichigo Ask Orihime Out
Jul 13, 2025
-
How Much Is 4 Oz Chocolate Chips
Jul 13, 2025
-
How Many Times Does 9 Go Into 70
Jul 13, 2025
-
4 Pics 1 Word Cheat 8 Letters
Jul 13, 2025
-
220 Kilometers Per Hour To Miles Per Hour
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about Find The Domain Of The Graphed Function Apex . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.