Find Y If X 4 Y 4 16
Kalali
Jun 14, 2025 · 3 min read
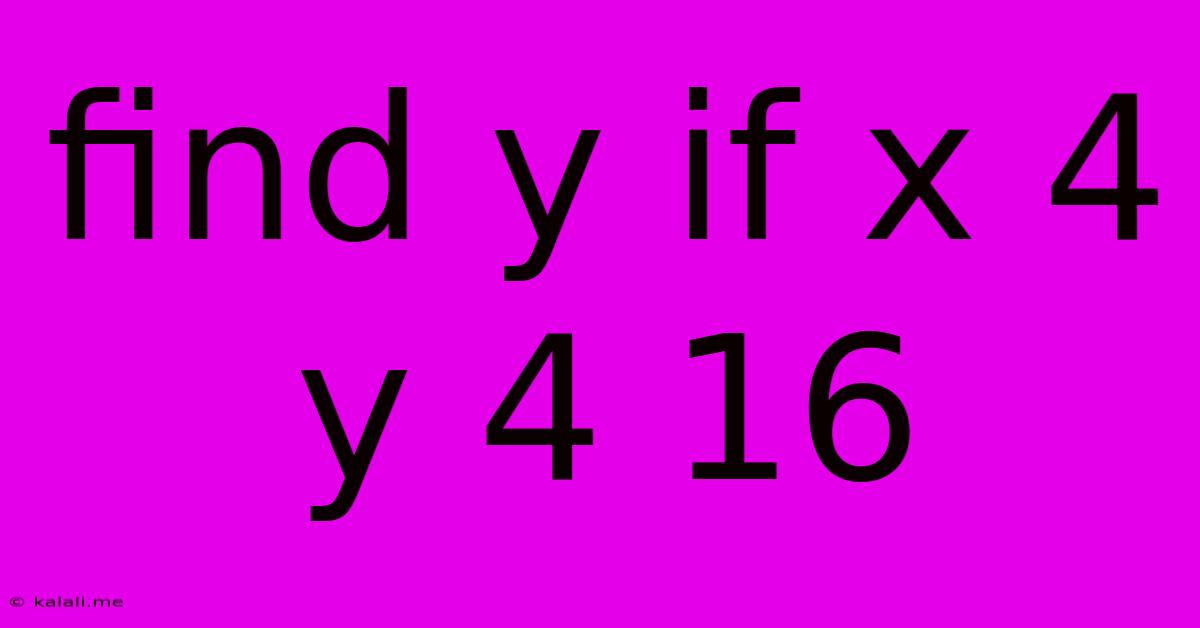
Table of Contents
Solving for y: Understanding x⁴ + y⁴ = 16
This article will guide you through solving the equation x⁴ + y⁴ = 16 for y. While there's no single, neat solution for y in terms of x (like y = f(x)), we can explore different approaches to understanding and representing the solution set. This problem delves into the complexities of higher-order equations and highlights the importance of considering the domain and range of the variables.
This equation represents a quartic curve. Understanding its properties is key to grasping the solutions. We can't simply isolate 'y' as we would in a linear equation. Instead, we explore various methods to find possible values for 'y' given a value for 'x'.
Methods for Solving x⁴ + y⁴ = 16
1. Rearranging the Equation:
The most straightforward approach is to rearrange the equation to solve for y⁴:
y⁴ = 16 - x⁴
Then, taking the fourth root of both sides gives us:
y = ±√(⁴√(16 - x⁴))
However, note the limitations. This equation is only defined when 16 - x⁴ ≥ 0. This implies that -2 ≤ x ≤ 2. Otherwise, we'd be taking the fourth root of a negative number, which results in complex numbers. Therefore, the real solutions for y are confined to this range of x values.
2. Graphical Representation:
Visualizing the equation graphically provides significant insight. Plotting the equation x⁴ + y⁴ = 16 reveals a closed curve symmetrical about both the x and y axes. This visual representation clearly shows the limitations on the values of x and y, reinforcing the constraint derived in the previous method. The graph helps demonstrate that for each x within the range [-2, 2], there are two corresponding values of y (positive and negative).
3. Numerical Methods:
For specific values of x, numerical methods such as the Newton-Raphson method can be used to approximate the solutions for y. This is particularly useful when an analytical solution is difficult or impossible to obtain. However, this approach provides only approximate solutions, not an exact algebraic expression.
4. Considering Complex Solutions:
If we expand the domain to include complex numbers, the solution set becomes far more extensive. For values of x outside the range [-2, 2], the solutions for y will involve complex numbers, expanding the possibilities considerably. This complicates the analysis but offers a more complete mathematical picture.
Understanding the Solution Set
The equation x⁴ + y⁴ = 16 represents a closed curve. The solution set describes all points (x, y) that lie on this curve. The key takeaway is that there isn't a single function y = f(x) that explicitly defines y in terms of x. Instead, for each value of x within the range [-2, 2], there are two corresponding real values of y, and infinitely many complex values if you consider the broader domain.
This problem underscores the importance of understanding the constraints imposed by the equation and utilizing appropriate methods to explore and represent the solution set. The choice of method will depend on the desired level of precision and the context of the problem. A graphical representation often provides the most intuitive understanding of the relationship between x and y.
Latest Posts
Latest Posts
-
Find The Area Of A Circle With Radius 28 Cm
Jun 15, 2025
-
Which Statement Is True About Ftp
Jun 15, 2025
-
How To Find The Largest Fraction
Jun 15, 2025
-
How Many Naturally Occurring Elements Are On Earth
Jun 15, 2025
-
What Is The Most Important Factor In Successful Learning
Jun 15, 2025
Related Post
Thank you for visiting our website which covers about Find Y If X 4 Y 4 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.