Finding The Area Of Composite Shapes
Kalali
Apr 05, 2025 · 6 min read
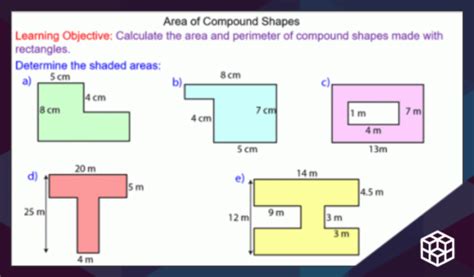
Table of Contents
Finding the Area of Composite Shapes: A Comprehensive Guide
Finding the area of simple shapes like squares, rectangles, and circles is straightforward. However, many real-world objects and designs involve composite shapes, which are formed by combining two or more basic shapes. Calculating the area of these composite shapes requires a strategic approach that combines understanding of basic area formulas with problem-solving skills. This comprehensive guide will equip you with the knowledge and techniques to master calculating the area of composite shapes.
Understanding Composite Shapes
A composite shape, also known as a complex shape, is a geometrical figure made up of two or more simple shapes. These simple shapes can be any combination of squares, rectangles, triangles, circles, semi-circles, trapezoids, and parallelograms. Identifying these individual shapes within the composite shape is the crucial first step in determining its total area.
Examples of Composite Shapes:
- A house shape (a rectangle with a triangle on top)
- An L-shaped room (two rectangles joined together)
- An irregular garden plot (a combination of rectangles and triangles)
- A pizza slice (a sector of a circle)
Strategies for Finding the Area of Composite Shapes
The core strategy for finding the area of composite shapes involves decomposition. This means breaking down the complex shape into its simpler constituent shapes. Once you've identified these simpler shapes, you can calculate their individual areas using standard formulas. Finally, you add or subtract these individual areas to find the total area of the composite shape.
Essential Area Formulas
Before diving into composite shapes, let's review the area formulas for common shapes:
- Rectangle: Area = length × width
- Square: Area = side × side (or side²)
- Triangle: Area = (1/2) × base × height
- Circle: Area = π × radius²
- Trapezoid: Area = (1/2) × (base1 + base2) × height
- Parallelogram: Area = base × height
Step-by-Step Approach to Solving Composite Shape Area Problems
Let's break down the process with a systematic approach:
-
Identify the constituent shapes: Carefully examine the composite shape and identify the simpler shapes that make it up. Sketch these individual shapes separately if it helps. Label relevant dimensions (length, width, height, radius, etc.) on your diagrams.
-
Calculate individual areas: Use the appropriate area formula for each identified shape. Remember to use consistent units (e.g., all measurements in centimeters or inches). Show your work clearly to minimize errors.
-
Add or subtract areas: Depending on how the shapes are combined, you'll either add or subtract the individual areas. If shapes are combined to form the larger shape, add their areas. If one shape is taken away from another (like a cutout), subtract the smaller area from the larger area.
-
State your answer: Clearly state the total area of the composite shape, including the appropriate units (e.g., square centimeters, square inches, square meters).
Examples: Finding the Area of Different Composite Shapes
Let's work through a few examples to illustrate these steps:
Example 1: L-Shaped Room
Imagine an L-shaped room with the following dimensions: One rectangular section is 10 feet long and 8 feet wide. The other rectangular section is 6 feet long and 4 feet wide. These two sections are joined to form the L-shape.
-
Constituent Shapes: Two rectangles.
-
Individual Areas:
- Rectangle 1: Area = 10 ft × 8 ft = 80 sq ft
- Rectangle 2: Area = 6 ft × 4 ft = 24 sq ft
-
Add or Subtract: Add the areas because the rectangles are joined together.
-
Total Area: Total area = 80 sq ft + 24 sq ft = 104 sq ft
Example 2: House Shape
Consider a house-shaped figure where the base is a rectangle with a length of 12 meters and a width of 8 meters, and the roof is an isosceles triangle with a base of 12 meters and a height of 5 meters.
-
Constituent Shapes: One rectangle and one triangle.
-
Individual Areas:
- Rectangle: Area = 12 m × 8 m = 96 sq m
- Triangle: Area = (1/2) × 12 m × 5 m = 30 sq m
-
Add or Subtract: Add the areas as the shapes form the whole figure.
-
Total Area: Total area = 96 sq m + 30 sq m = 126 sq m
Example 3: Irregular Garden Plot
Suppose a garden plot is composed of a rectangle with a length of 15 feet and a width of 10 feet, and a semi-circle with a diameter of 10 feet attached to one of the rectangle's sides.
-
Constituent Shapes: One rectangle and one semi-circle.
-
Individual Areas:
- Rectangle: Area = 15 ft × 10 ft = 150 sq ft
- Semi-circle: Radius = 10 ft / 2 = 5 ft; Area = (1/2) × π × (5 ft)² ≈ 39.27 sq ft
-
Add or Subtract: Add the areas since both contribute to the garden plot's size.
-
Total Area: Total area ≈ 150 sq ft + 39.27 sq ft ≈ 189.27 sq ft
Example 4: Shape with a Cutout
Let's consider a square with side length 10 cm and a smaller square cutout with side length 4 cm.
-
Constituent Shapes: A large square and a smaller square.
-
Individual Areas:
- Large square: Area = 10 cm × 10 cm = 100 sq cm
- Small square: Area = 4 cm × 4 cm = 16 sq cm
-
Add or Subtract: Subtract the smaller area from the larger area.
-
Total Area: Total area = 100 sq cm - 16 sq cm = 84 sq cm
Advanced Composite Shapes and Strategies
Some composite shapes might require more advanced strategies. These include:
-
Using coordinates: If the shape's vertices are defined by coordinates on a grid, you can use coordinate geometry techniques to calculate the areas of triangles and other polygons within the composite shape.
-
Dividing into multiple shapes: For highly irregular shapes, you might need to divide them into several smaller, simpler shapes before calculating their individual areas and summing them up.
-
Approximation: For extremely complex shapes, you might need to use approximation methods, such as dividing the shape into small squares or rectangles and estimating the total area.
Practical Applications of Composite Shape Area Calculations
Understanding how to calculate the area of composite shapes is crucial in many fields, including:
- Construction: Estimating material requirements for flooring, roofing, painting, etc.
- Engineering: Calculating surface areas and volumes of complex structures.
- Architecture: Designing floor plans and calculating the area of rooms and buildings.
- Gardening and Landscaping: Designing and calculating the area of gardens, patios, and other outdoor spaces.
- Manufacturing: Calculating material usage in various manufacturing processes.
Conclusion
Mastering the calculation of the area of composite shapes is a valuable skill with wide-ranging applications. By systematically breaking down complex shapes into simpler components, and utilizing the appropriate area formulas, you can accurately determine the area of even the most intricate designs. Remember to always clearly label your diagrams, show your working, and state your answer with the correct units. Practice will significantly improve your proficiency and confidence in tackling these types of problems. The more you practice, the more intuitively you will be able to identify the constituent shapes and apply the correct formulas. Keep practicing, and you’ll become a composite shape area calculation expert in no time!
Latest Posts
Latest Posts
-
Convert 12 Degrees Celsius To Fahrenheit
Apr 06, 2025
-
Aluminum Foil Mixture Or Pure Substance
Apr 06, 2025
-
Cual Es El 20 De 20
Apr 06, 2025
-
What Is The Difference Between Community And Population
Apr 06, 2025
-
What Is 72 Degrees F In Celsius
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Finding The Area Of Composite Shapes . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
