Finding The Hole Of A Rational Function
Kalali
Mar 28, 2025 · 6 min read
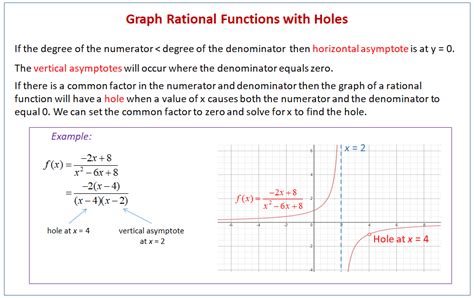
Table of Contents
Finding the Holes of a Rational Function: A Comprehensive Guide
Rational functions, defined as the ratio of two polynomial functions, often exhibit unique characteristics like vertical asymptotes and holes. While asymptotes represent values where the function approaches infinity, holes signify points of discontinuity where the function is undefined but can be "filled" by defining the function at that specific point. Identifying these holes is crucial for accurately graphing and analyzing rational functions. This comprehensive guide delves into the intricacies of finding holes in rational functions, equipping you with the necessary tools and techniques.
Understanding Rational Functions and Their Components
Before diving into the process of finding holes, let's solidify our understanding of rational functions. A rational function is expressed in the form:
f(x) = p(x) / q(x)
where p(x) and q(x) are polynomial functions, and q(x) is not the zero polynomial (otherwise, it wouldn't be a function).
Rational functions can possess several key features:
-
Vertical Asymptotes: These occur when the denominator q(x) is equal to zero, and the numerator p(x) is not zero at the same point. The function approaches positive or negative infinity as x approaches the vertical asymptote.
-
Horizontal Asymptotes: These describe the behavior of the function as x approaches positive or negative infinity. The existence and value of a horizontal asymptote depend on the degrees of the numerator and denominator polynomials.
-
Holes (Removable Discontinuities): These are points where the function is undefined, but the discontinuity can be removed by defining the function at that specific point. Holes occur when both the numerator and denominator share a common factor that can be canceled out.
-
x-intercepts: These are points where the function crosses the x-axis, i.e., where f(x) = 0. This happens when the numerator p(x) is equal to zero, and the denominator q(x) is not zero.
-
y-intercept: This is the point where the function crosses the y-axis, i.e., where x = 0. It's found by calculating f(0), provided q(0) is not zero.
Identifying and Locating Holes: A Step-by-Step Approach
The key to finding holes in a rational function lies in factorization. If both the numerator and denominator share a common factor, that factor represents a potential hole. Let's break down the process:
Step 1: Factor Both the Numerator and the Denominator
Completely factor both p(x) and q(x) into their simplest forms. This often involves techniques like factoring quadratics, grouping, or using the rational root theorem for higher-degree polynomials. For example:
f(x) = (x² - 4) / (x² - x - 2)
Factoring, we get:
f(x) = (x - 2)(x + 2) / (x - 2)(x + 1)
Step 2: Identify Common Factors
Examine the factored numerator and denominator for any common factors. In our example, (x - 2) is a common factor.
Step 3: Cancel Out Common Factors
Carefully cancel out the common factors from both the numerator and denominator. This step is crucial in revealing the location of the hole.
f(x) = (x + 2) / (x + 1), x ≠ 2
Notice the condition x ≠ 2. This is because the original function is undefined at x = 2.
Step 4: Determine the x-coordinate of the Hole
The x-coordinate of the hole is the value of x that makes the canceled common factor equal to zero. In our example:
x - 2 = 0 => x = 2
Therefore, the hole occurs at x = 2.
Step 5: Determine the y-coordinate of the Hole
To find the y-coordinate, substitute the x-coordinate of the hole into the simplified rational function (after canceling the common factor):
y = (2 + 2) / (2 + 1) = 4/3
Therefore, the hole is located at the point (2, 4/3).
Illustrative Examples: Diverse Cases of Hole Identification
Let's explore a few more examples to solidify our understanding:
Example 1: A Simpler Case
f(x) = (x + 3)(x - 1) / (x - 1)(x + 2)
Here, the common factor is (x - 1). Cancelling it out:
f(x) = (x + 3) / (x + 2), x ≠ 1
The hole is at x = 1. Substituting into the simplified function:
y = (1 + 3) / (1 + 2) = 4/3
The hole is located at (1, 4/3).
Example 2: A Case with Multiple Holes (Rare but Possible)
Consider a more complex scenario where the numerator and denominator share multiple common factors:
f(x) = (x - 2)²(x + 5) / (x - 2)(x + 5)(x + 1)
We can cancel out (x - 2) and (x + 5):
f(x) = 1 / (x + 1), x ≠ 2, x ≠ -5
This function has holes at x = 2 and x = -5. Substituting these values into the simplified function gives us the corresponding y-coordinates:
For x = 2: y = 1/(2 + 1) = 1/3 => Hole at (2, 1/3)
For x = -5: y = 1/(-5 + 1) = -1/4 => Hole at (-5, -1/4)
Example 3: A Case with No Holes
Not all rational functions have holes. If the numerator and denominator share no common factors after factorization, there will be no holes. For instance:
f(x) = (x² + 1) / (x - 3)
This function has no common factors between the numerator and denominator and thus has no holes.
Advanced Techniques and Considerations
While factorization is the primary method, certain situations might require more advanced techniques:
-
Long Division: For higher-degree polynomials where factoring proves difficult, long division can help reveal hidden common factors.
-
Synthetic Division: A more efficient alternative to long division for dividing by linear factors.
-
Partial Fraction Decomposition: For more complex rational functions, partial fraction decomposition can simplify the expression and make identifying common factors easier.
The Significance of Holes in Graphing and Analysis
Understanding holes is critical for accurate graphing and analysis of rational functions:
-
Accurate Graphing: Holes represent points of discontinuity that need to be explicitly indicated on the graph. They are typically represented as open circles at the precise location of the hole.
-
Domain and Range: Holes affect the domain (possible input values) of the rational function. The x-coordinate of the hole is excluded from the domain. The range (possible output values) might also be affected, especially if the y-coordinate of the hole corresponds to a specific value.
Conclusion: Mastering the Art of Hole Identification
Finding the holes of a rational function is a fundamental skill in calculus and algebra. By mastering factorization techniques and applying the step-by-step approach outlined in this guide, you can accurately identify and locate these crucial points of discontinuity. Remember that the presence or absence of holes significantly influences the graph, domain, and range of a rational function. Understanding this concept opens the door to a deeper understanding of rational function behavior and their applications in various fields, including engineering, physics, and economics. Practice is key; the more you work through examples, the more comfortable you’ll become with identifying these crucial features of rational functions.
Latest Posts
Latest Posts
-
7am To 11am Is How Many Hours
Jul 12, 2025
-
If Your 35 What Year Was You Born
Jul 12, 2025
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
-
30 X 30 Is How Many Square Feet
Jul 12, 2025
-
How Much Does A Half Oz Weigh
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about Finding The Hole Of A Rational Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.