Finding The Magnitude Of A Force
Kalali
Apr 06, 2025 · 6 min read
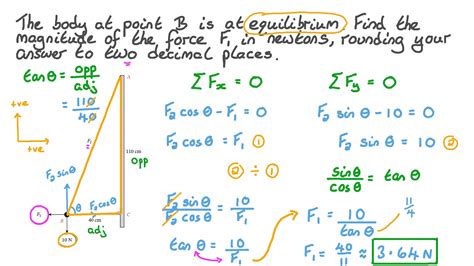
Table of Contents
Finding the Magnitude of a Force: A Comprehensive Guide
Understanding and calculating the magnitude of a force is fundamental in physics and engineering. Forces, being vector quantities, possess both magnitude (size) and direction. While the direction is crucial for understanding the effect of a force, determining its magnitude is often the first step in solving many physical problems. This comprehensive guide explores various methods for finding the magnitude of a force, covering both simple and complex scenarios.
Understanding Forces and Vectors
Before delving into the methods, let's solidify our understanding of forces and vectors. A force is an interaction that, when unopposed, will change the motion of an object. It's a push or a pull. Crucially, force is a vector quantity. This means it's fully described by both its magnitude (how strong it is) and its direction. We represent vectors graphically as arrows, where the length of the arrow corresponds to the magnitude and the arrowhead indicates the direction.
Representing Forces: Vector Notation
Forces are commonly represented using vector notation. A common notation uses bold letters (e.g., F) to denote a vector. The magnitude of the vector is then represented by the same letter, but without the boldface (e.g., F or |F|). This distinction is crucial to avoid confusion.
Methods for Finding the Magnitude of a Force
The method used to determine the magnitude of a force depends on the context and the information available. Here are several common approaches:
1. Direct Measurement Using a Force Meter (Spring Scale)
The simplest way to find the magnitude of a force is through direct measurement. A force meter, also known as a spring scale, directly measures the force applied to it. The reading on the scale gives the magnitude of the force in units like Newtons (N). This method is suitable for relatively simple, static forces.
2. Using Newton's Second Law (F = ma)
Newton's second law of motion, F = ma, provides a powerful method for calculating the magnitude of a force. If we know the mass (m) of an object and its acceleration (a), we can calculate the net force (F) acting on it.
- F: The net force acting on the object (in Newtons, N)
- m: The mass of the object (in kilograms, kg)
- a: The acceleration of the object (in meters per second squared, m/s²)
Example: A 2 kg object accelerates at 5 m/s². The net force acting on it is:
F = ma = (2 kg)(5 m/s²) = 10 N
Important Note: This method calculates the net force – the vector sum of all forces acting on the object. If multiple forces are involved, resolving them into components (as discussed below) is crucial before applying F=ma.
3. Resolving Forces into Components and Using Trigonometry
When dealing with forces acting at angles, resolving them into their x and y components is essential. This involves using trigonometry. Once the components are found, the magnitude of the resultant force can be calculated using the Pythagorean theorem.
Let's consider a force F acting at an angle θ with respect to the horizontal x-axis.
- F<sub>x</sub> = F cos θ: The x-component of the force.
- F<sub>y</sub> = F sin θ: The y-component of the force.
The magnitude of the resultant force (F) is then:
F = √(F<sub>x</sub>² + F<sub>y</sub>²)
Example: A force of 10 N acts at an angle of 30° to the horizontal.
- F<sub>x</sub> = 10 N * cos(30°) ≈ 8.66 N
- F<sub>y</sub> = 10 N * sin(30°) = 5 N
The magnitude of the force is:
F = √(8.66² + 5²) ≈ 10 N (This confirms our initial force magnitude)
4. Vector Addition: Finding the Resultant Force
If multiple forces act on an object simultaneously, we need to find the resultant force – the single force that produces the same effect as all the individual forces combined. This involves vector addition.
Graphical Method: Forces can be added graphically using the head-to-tail method. Draw each force vector to scale, placing the tail of the next vector at the head of the previous one. The resultant force is the vector drawn from the tail of the first vector to the head of the last vector. Its magnitude can then be measured directly from the diagram.
Analytical Method: For greater precision, use the component method. Resolve each force into its x and y components. Sum the x-components separately and the y-components separately. The resultant force's x and y components are these sums. Then use the Pythagorean theorem to find the magnitude of the resultant force.
Example (Analytical): Two forces, F<sub>1</sub> = 5 N (at 0°) and F<sub>2</sub> = 12 N (at 90°), act on an object.
- F<sub>1x</sub> = 5 N, F<sub>1y</sub> = 0 N
- F<sub>2x</sub> = 0 N, F<sub>2y</sub> = 12 N
Resultant components:
- F<sub>Rx</sub> = F<sub>1x</sub> + F<sub>2x</sub> = 5 N
- F<sub>Ry</sub> = F<sub>1y</sub> + F<sub>2y</sub> = 12 N
Magnitude of the resultant force:
F<sub>R</sub> = √(5² + 12²) = 13 N
5. Using Equilibrium Conditions
If an object is in static equilibrium, the net force acting on it is zero. This means the vector sum of all forces is zero. This condition can be used to determine the magnitude of an unknown force if the other forces are known.
Example: A weight of 100 N hangs from a rope. Two other ropes support the weight, each making an angle of 30° with the vertical. By resolving forces and applying equilibrium conditions (ΣFx = 0 and ΣFy = 0), we can determine the tension in each of the supporting ropes.
Advanced Scenarios and Considerations
The methods described above cover many common situations. However, more complex scenarios may require advanced techniques:
- Non-inertial frames of reference: If the frame of reference is accelerating, fictitious forces (like centrifugal force) need to be considered.
- Rotating systems: Centripetal and tangential forces come into play.
- Deformable bodies: Internal forces within the object must be accounted for.
- Three-dimensional forces: Vector addition and component resolution become more complex in three dimensions, often requiring matrix algebra.
Practical Applications
Finding the magnitude of a force is vital in numerous fields:
- Engineering: Structural analysis, bridge design, machine design all rely heavily on understanding and calculating forces.
- Physics: Solving problems in mechanics, dynamics, and electromagnetism often involves determining the magnitudes of forces.
- Aerospace: Aircraft design, rocket propulsion, and satellite trajectories necessitate precise force calculations.
- Biomechanics: Analyzing human movement, designing prosthetics, and understanding muscle function all require an understanding of forces.
Conclusion
Determining the magnitude of a force is a fundamental skill in many scientific and engineering disciplines. While a simple spring scale might suffice for direct measurements of simple forces, more complex scenarios require a deeper understanding of vector algebra, trigonometry, and Newton's laws of motion. Mastering these techniques allows for accurate calculations crucial for problem-solving in various fields. Remember to always carefully consider the context of the problem and choose the appropriate method for calculating the magnitude of the force. The examples provided offer a solid foundation, but further exploration of vector calculus will be beneficial for tackling more advanced scenarios.
Latest Posts
Latest Posts
-
What Is 20 Percent Off Of 39 99
Jul 03, 2025
-
Where Is The 3 In Riddle Transfer
Jul 03, 2025
-
How Much Does A Water Bottle Weight
Jul 03, 2025
-
How Many Inches Is Half A Yard
Jul 03, 2025
-
How Old Are You If Your Born In 1996
Jul 03, 2025
Related Post
Thank you for visiting our website which covers about Finding The Magnitude Of A Force . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.