Finding Zeros Of A Function Fraction
Kalali
Apr 01, 2025 · 6 min read
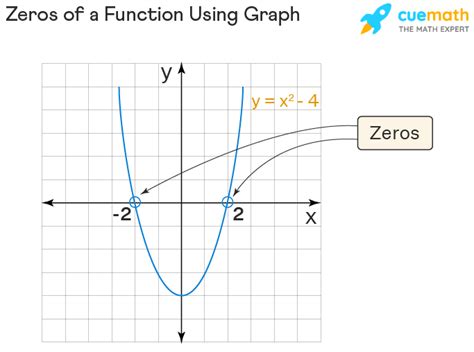
Table of Contents
Finding Zeros of a Function Fraction: A Comprehensive Guide
Finding the zeros of a function, especially a rational function (a fraction of two functions), is a crucial skill in algebra and calculus. Zeros, also known as roots or x-intercepts, represent the values of x where the function's output (y-value) is equal to zero. This article will provide a comprehensive guide on how to find the zeros of a function fraction, covering various techniques and complexities. We will explore different approaches, highlighting the importance of understanding the underlying concepts and utilizing strategic problem-solving techniques.
Understanding Rational Functions and Their Zeros
A rational function is defined as the ratio of two polynomial functions, typically expressed as:
f(x) = P(x) / Q(x)
where P(x) and Q(x) are polynomials, and Q(x) is not identically zero. The zeros of a rational function occur when the entire function equals zero. Since a fraction is equal to zero only when its numerator is zero and its denominator is non-zero, finding the zeros of a rational function involves a two-step process:
-
Find the zeros of the numerator: Set the numerator P(x) equal to zero and solve for x. These solutions are potential zeros of the rational function.
-
Check for undefined points: Ensure that none of the potential zeros are also zeros of the denominator Q(x). If a value makes both the numerator and denominator zero, it's not a zero of the rational function; it's a point of discontinuity (often a hole in the graph).
Methods for Finding Zeros of Polynomial Numerators
Finding the zeros of the numerator polynomial, P(x), can involve several techniques depending on the degree and complexity of the polynomial:
1. Factoring
Factoring is the most straightforward method for finding zeros, especially for quadratic and some cubic polynomials. If you can factor P(x) into linear factors, setting each factor to zero will give you the zeros.
Example:
Let's say the numerator of our rational function is:
P(x) = x² - 5x + 6
Factoring this quadratic gives:
P(x) = (x - 2)(x - 3)
Setting each factor to zero:
x - 2 = 0 => x = 2
x - 3 = 0 => x = 3
Therefore, the zeros of P(x) are 2 and 3.
2. Quadratic Formula
For quadratic polynomials that don't factor easily, the quadratic formula provides a reliable method to find the zeros:
For a quadratic equation of the form ax² + bx + c = 0, the zeros are given by:
x = [-b ± √(b² - 4ac)] / 2a
The discriminant (b² - 4ac) determines the nature of the zeros:
- b² - 4ac > 0: Two distinct real zeros.
- b² - 4ac = 0: One real zero (a repeated root).
- b² - 4ac < 0: Two complex conjugate zeros.
3. Cubic and Higher-Degree Polynomials
Finding zeros of cubic and higher-degree polynomials can be more challenging. Methods include:
- Factoring by grouping: This technique works for some polynomials that can be grouped into smaller, factorable expressions.
- Synthetic division: This method efficiently tests potential rational zeros (zeros that are rational numbers).
- Numerical methods: For polynomials that don't factor easily, numerical methods like the Newton-Raphson method can approximate the zeros.
- Using technology: Graphing calculators or computer algebra systems (CAS) can efficiently find zeros of higher-degree polynomials.
Handling the Denominator: Points of Discontinuity
After identifying the potential zeros from the numerator, it's crucial to examine the denominator, Q(x). Any value of x that makes the denominator zero is a point of discontinuity. These points are not zeros of the rational function because division by zero is undefined.
There are two types of discontinuities:
-
Holes: If a value of x makes both the numerator and the denominator zero, it represents a hole in the graph. This occurs when a common factor can be cancelled out from both the numerator and denominator.
-
Vertical Asymptotes: If a value of x makes only the denominator zero, it represents a vertical asymptote. The function approaches positive or negative infinity as x approaches this value.
Example:
Consider the rational function:
f(x) = (x² - 4) / (x - 2)
Factoring the numerator:
f(x) = (x - 2)(x + 2) / (x - 2)
We can cancel out the (x - 2) term, provided x ≠ 2:
f(x) = x + 2, x ≠ 2
The simplified function has a zero at x = -2. However, at x = 2, there is a hole because both the numerator and denominator were originally zero at x = 2.
Advanced Techniques and Considerations
Partial Fraction Decomposition
For complex rational functions, partial fraction decomposition can simplify the expression, making it easier to find zeros. This technique breaks down a rational function into a sum of simpler fractions.
Oblique Asymptotes
Rational functions where the degree of the numerator is greater than the degree of the denominator have oblique (slant) asymptotes. These asymptotes don't affect the zeros of the function, but they are important for understanding the overall behavior of the graph.
Complex Zeros
Polynomials can have complex zeros (involving the imaginary unit 'i'). These zeros often come in conjugate pairs (a + bi and a - bi). Complex zeros are important in certain applications, but they don't represent x-intercepts on the real number plane.
Step-by-Step Example: Finding Zeros of a Complex Rational Function
Let's find the zeros of the following rational function:
f(x) = (x³ - 6x² + 11x - 6) / (x² - 5x + 6)
Step 1: Factor the Numerator
The numerator is a cubic polynomial. We can use synthetic division or other methods to find its roots. By testing integer factors of the constant term (-6), we find that x = 1, x = 2, and x = 3 are roots. Therefore:
x³ - 6x² + 11x - 6 = (x - 1)(x - 2)(x - 3)
Step 2: Factor the Denominator
The denominator is a quadratic polynomial. Factoring gives:
x² - 5x + 6 = (x - 2)(x - 3)
Step 3: Simplify and Identify Zeros
The rational function becomes:
f(x) = (x - 1)(x - 2)(x - 3) / (x - 2)(x - 3)
We can cancel out the (x - 2) and (x - 3) terms, provided x ≠ 2 and x ≠ 3:
f(x) = x - 1, x ≠ 2, x ≠ 3
The simplified function has a zero at x = 1. At x = 2 and x = 3, there are holes in the graph because these values make both the numerator and denominator zero in the original function.
Conclusion
Finding the zeros of a function fraction involves a systematic approach combining polynomial factoring, the quadratic formula, and an understanding of discontinuities. By carefully analyzing the numerator and denominator, you can identify the zeros and points of discontinuity, leading to a complete understanding of the function's behavior. Remember to always check for holes and vertical asymptotes to get a comprehensive picture of the function's graph. Mastering these techniques is essential for success in algebra, calculus, and various applications in science and engineering. This thorough guide equips you with the knowledge and tools to tackle a wide range of problems related to finding zeros of rational functions. Remember to practice regularly to build proficiency and confidence in this important mathematical skill.
Latest Posts
Latest Posts
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
-
How Many Dimes In A 5 Roll
Jul 18, 2025
-
How Do You Say Basil In Spanish
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about Finding Zeros Of A Function Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.