Four More Than A Number Is More Than 13
Kalali
Jul 23, 2025 · 6 min read
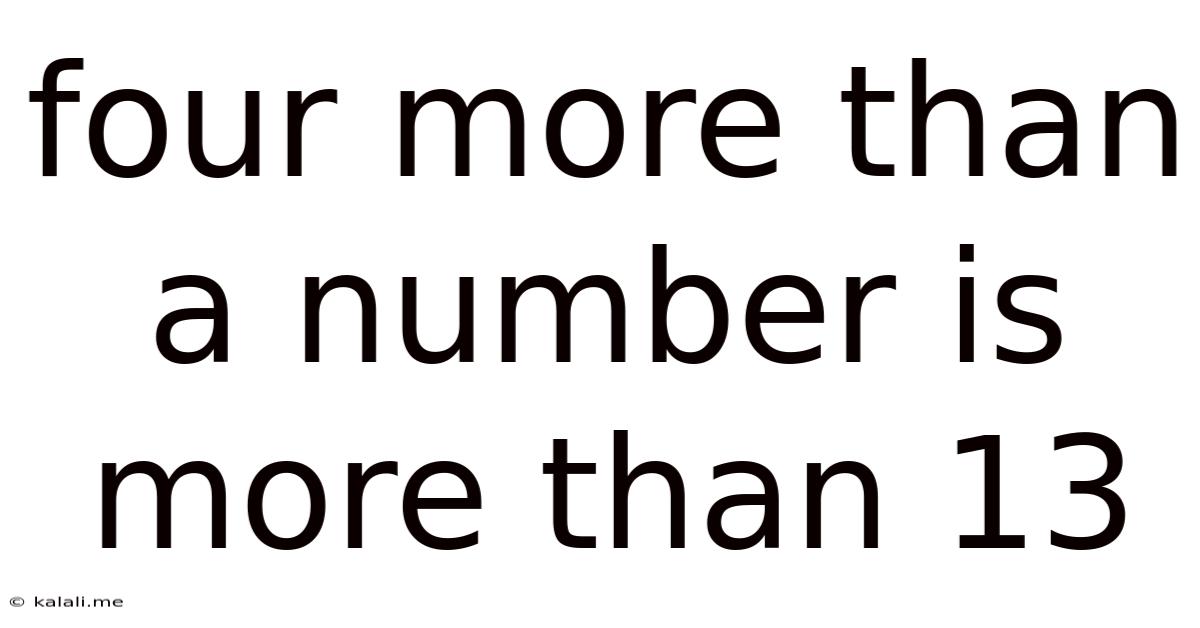
Table of Contents
Four More Than a Number is More Than 13: A Deep Dive into Inequalities
This article explores the mathematical inequality "four more than a number is more than 13," translating it into algebraic form, solving it, and then extending the concept to encompass more complex scenarios and real-world applications. We'll delve into the nuances of inequalities, graphing solutions, and understanding the implications of different inequality symbols. This exploration will be beneficial for students learning algebra and anyone interested in improving their mathematical problem-solving skills.
Meta Description: Learn how to solve the inequality "four more than a number is more than 13." This comprehensive guide covers algebraic representation, solution methods, graphing, and real-world applications, perfect for algebra students and anyone wanting to strengthen their math skills.
Understanding the Problem: From Words to Algebra
The phrase "four more than a number" immediately suggests addition. Let's represent the unknown number with the variable x. Therefore, "four more than a number" can be written algebraically as x + 4. The phrase "is more than 13" indicates an inequality, specifically a "greater than" relationship. This translates to the symbol >. Putting it all together, the complete inequality is:
x + 4 > 13
This simple equation forms the foundation for our exploration. We'll now proceed to solve it and interpret the solution.
Solving the Inequality: Isolating the Variable
Solving inequalities is very similar to solving equations. The goal is to isolate the variable (x in this case) on one side of the inequality sign. To do this, we perform inverse operations. In our inequality, x + 4 > 13, the constant 4 is added to x. The inverse operation of addition is subtraction. We subtract 4 from both sides of the inequality to maintain balance:
x + 4 - 4 > 13 - 4
This simplifies to:
x > 9
This means that any number greater than 9 satisfies the original inequality. Let's test this with a few examples:
- x = 10: 10 + 4 = 14, which is greater than 13. This satisfies the inequality.
- x = 9: 9 + 4 = 13, which is not greater than 13. This does not satisfy the inequality. Note that 9 is not included in the solution set because the inequality is strictly "greater than," not "greater than or equal to."
- x = 8: 8 + 4 = 12, which is not greater than 13. This does not satisfy the inequality.
Graphing the Solution: Visual Representation
Inequalities can be visually represented on a number line. To graph the solution x > 9, we draw a number line, locate the number 9, and then draw an open circle at 9. The open circle indicates that 9 is not included in the solution set. We then shade the region to the right of 9, representing all numbers greater than 9.
[Imagine a number line here with an open circle at 9 and shading to the right]
Exploring Different Inequality Symbols: ≥ and ≤
The inequality we've solved uses the "greater than" symbol (>). However, other inequality symbols exist:
-
Greater than or equal to (≥): This symbol indicates that the solution includes the value itself. For example, if the inequality were
x + 4 ≥ 13, the solution would bex ≥ 9, and the graph would include a closed circle at 9 on the number line. -
Less than (<): This symbol indicates that the solution includes all values less than a given value, excluding the value itself.
-
Less than or equal to (≤): This symbol includes the given value in the solution set.
More Complex Inequalities: Multiple Steps
Let's consider a slightly more complex scenario: "Three times a number, minus two, is less than or equal to seven."
This translates to the inequality:
3x - 2 ≤ 7
To solve this:
- Add 2 to both sides:
3x ≤ 9 - Divide both sides by 3:
x ≤ 3
The solution is x ≤ 3, meaning any number less than or equal to 3 satisfies the inequality. The graph would show a closed circle at 3, with shading to the left.
Real-World Applications: Word Problems and Scenarios
Inequalities have numerous real-world applications. Consider these examples:
-
Budgeting: You have $50 to spend on groceries. If apples cost $2 per pound, how many pounds of apples can you buy? This translates to the inequality
2x ≤ 50, where x represents the number of pounds of apples. Solving this yieldsx ≤ 25. You can buy 25 pounds or less. -
Speed Limits: The speed limit is 65 mph. This can be represented as
x ≤ 65, where x is your speed. Driving faster than 65 mph is a violation. -
Grades: To pass a course, you need an average grade of at least 70%. If you have scores of 65, 78, and 82 on three assignments, what score do you need on the fourth assignment to pass? Let x be the score on the fourth assignment. The inequality is:
(65 + 78 + 82 + x)/4 ≥ 70. Solving this requires multiple steps, leading tox ≥ 75. -
Sales Targets: A salesperson needs to sell at least 100 units to reach their bonus target. If they've already sold 75 units, how many more units do they need to sell? This inequality is
x + 75 ≥ 100, which solves tox ≥ 25.
These examples demonstrate the practical utility of understanding and solving inequalities.
Compound Inequalities: Combining Multiple Conditions
We can also encounter compound inequalities, which combine two or more inequalities. For instance:
5 < x + 2 < 10
This means that x + 2 is greater than 5 and less than 10. To solve this, we subtract 2 from all parts of the inequality:
5 - 2 < x < 10 - 2
3 < x < 7
This means x is greater than 3 and less than 7. The solution is all numbers between 3 and 7, excluding 3 and 7 themselves. The graph would show open circles at 3 and 7, with shading in between.
Absolute Value Inequalities: A Further Challenge
Absolute value inequalities introduce another layer of complexity. The absolute value of a number is its distance from zero, always positive. For example, |3| = 3 and |-3| = 3. Let's consider:
|x - 2| < 5
This means the distance between x and 2 is less than 5. To solve this, we consider two separate inequalities:
x - 2 < 5 and x - 2 > -5
Solving each yields:
x < 7 and x > -3
Combining these, we get -3 < x < 7. This signifies that x is between -3 and 7, excluding -3 and 7.
Conclusion: Mastering Inequalities for Mathematical Proficiency
This comprehensive exploration of inequalities, from the simple "four more than a number is more than 13" to more complex scenarios involving compound and absolute value inequalities, highlights the fundamental importance of this concept in algebra and its widespread applications in real-world problems. Mastering the techniques presented here will significantly enhance your mathematical problem-solving abilities and provide a solid foundation for tackling more advanced mathematical concepts. Remember to practice regularly and apply these principles to diverse problems to fully solidify your understanding. The ability to translate word problems into algebraic inequalities and then solve them efficiently is a crucial skill for success in mathematics and beyond.
Latest Posts
Latest Posts
-
How Much Does A Pint Of Cherry Tomatoes Weigh
Jul 23, 2025
-
How Many Cups Is 15 Ounces Of Pumpkin
Jul 23, 2025
-
Whats A Goon To A Goblin Meaning
Jul 23, 2025
-
How Many 1 8 Teaspoons Are In 1 Teaspoon
Jul 23, 2025
-
How Many Grams In Teaspoon Of Peanut Butter
Jul 23, 2025
Related Post
Thank you for visiting our website which covers about Four More Than A Number Is More Than 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.