Graph Of 1 X 2 Y 2
Kalali
May 21, 2025 · 2 min read
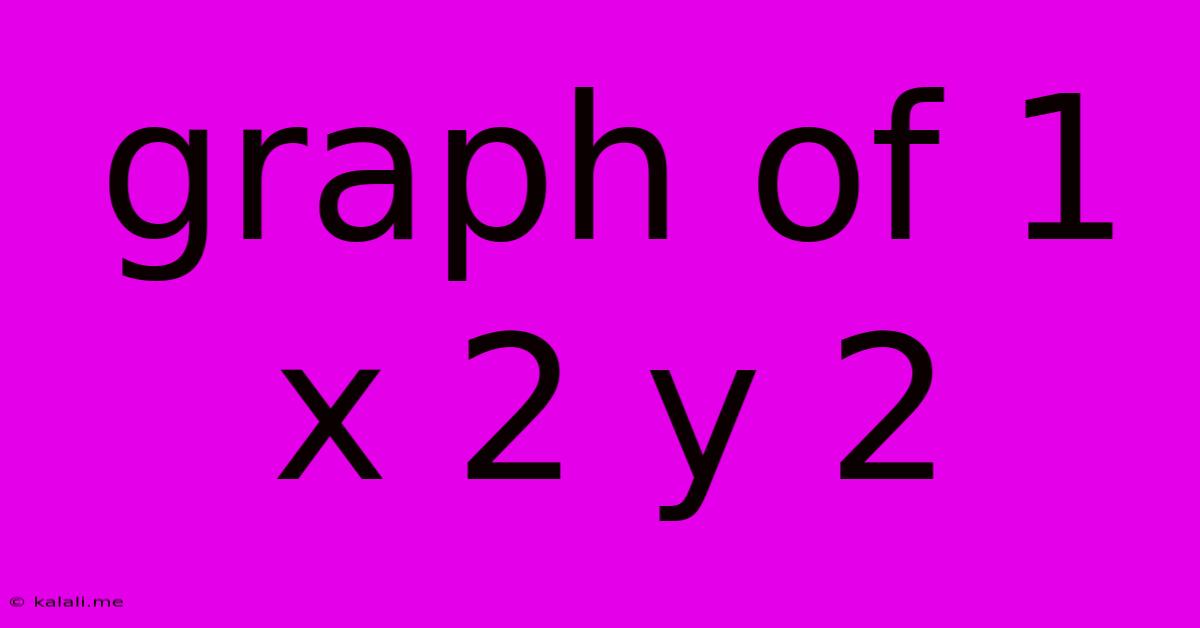
Table of Contents
Understanding the Graph of 1x² + 2y²
The equation 1x² + 2y² represents an ellipse, a specific type of conic section. This article will explore its characteristics, how to graph it, and its key features. Understanding this equation is crucial for anyone studying conic sections, analytic geometry, or related mathematical fields.
Key Features and Characteristics of the Ellipse
The general equation for an ellipse centered at the origin is:
(x²/a²) + (y²/b²) = 1
Where 'a' and 'b' represent the lengths of the semi-major and semi-minor axes, respectively. Comparing this to our equation, 1x² + 2y² = 1, we can rewrite it in the standard form:
x²/1 + y²/(1/2) = 1
From this, we can identify:
- a² = 1, therefore a = 1 (length of the semi-major axis along the x-axis)
- b² = 1/2, therefore b = 1/√2 ≈ 0.707 (length of the semi-minor axis along the y-axis)
This means the ellipse is elongated along the x-axis. The major axis has a length of 2a = 2, and the minor axis has a length of 2b = √2. The foci are located along the major axis, inside the ellipse.
Calculating the Foci
The distance from the center to each focus (c) can be calculated using the relationship:
c² = a² - b² = 1 - (1/2) = 1/2
Therefore, c = 1/√2 ≈ 0.707. The foci are located at approximately (±0.707, 0).
Graphing the Ellipse
To graph the ellipse, follow these steps:
- Plot the center: The center of the ellipse is at the origin (0, 0).
- Plot the vertices: The vertices are located at (±a, 0), which are (±1, 0) in this case.
- Plot the co-vertices: The co-vertices are located at (0, ±b), which are approximately (0, ±0.707).
- Sketch the ellipse: Using the vertices and co-vertices as guides, sketch a smooth, oval-shaped curve. Remember the ellipse is symmetrical about both the x and y axes.
Understanding the Equation's Implications
The coefficients of x² and y² in the equation dictate the shape and orientation of the ellipse. A larger coefficient indicates a shorter axis. In this case, the larger coefficient for x² indicates that the ellipse is wider along the x-axis.
Further Exploration
This analysis provides a foundational understanding of the graph of 1x² + 2y² = 1. Further exploration could involve:
- Examining transformations of the equation (e.g., translations, rotations).
- Exploring the relationship between the ellipse's equation and its eccentricity.
- Applying this knowledge to solve real-world problems involving elliptical shapes.
By understanding the standard form of the ellipse equation and applying the steps outlined above, you can accurately graph and analyze this specific conic section. This knowledge is essential for various mathematical applications.
Latest Posts
Latest Posts
-
Wiring A Extractor Fan With Timer
May 21, 2025
-
Can A Woman Travel Alone In Islam
May 21, 2025
-
None So Blind As Those That Will Not See
May 21, 2025
-
1 Light 2 Switch Wiring Diagram
May 21, 2025
-
Can You Get Fleas Without Pets
May 21, 2025
Related Post
Thank you for visiting our website which covers about Graph Of 1 X 2 Y 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.