Graph Shows A System Of Equations With Infinitely Many Solutions
Kalali
Mar 27, 2025 · 6 min read
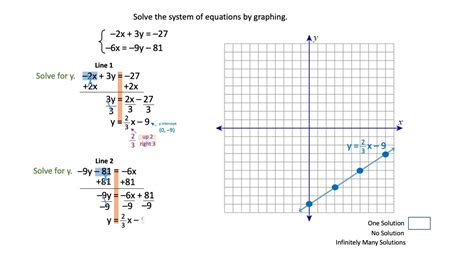
Table of Contents
Graph Shows a System of Equations with Infinitely Many Solutions: A Comprehensive Guide
Understanding systems of equations is fundamental to various fields, from engineering and physics to economics and computer science. A key concept within this realm is the notion of a system possessing infinitely many solutions. This article delves into the graphical representation and algebraic understanding of such systems, providing a comprehensive guide for students and enthusiasts alike.
What Does it Mean to Have Infinitely Many Solutions?
A system of equations is a collection of two or more equations that involve the same set of variables. A solution to the system is a set of values for the variables that simultaneously satisfies all equations in the system. When a system has infinitely many solutions, it means there are an infinite number of sets of values for the variables that satisfy all equations. This doesn't mean any random values will work; rather, the solutions are related in a specific way, forming a continuous set of solutions.
This contrasts with a system having:
- A unique solution: One and only one set of values satisfies the equations.
- No solution: No set of values satisfies all equations simultaneously.
Graphical Representation of Infinitely Many Solutions
The graphical representation of a system of equations offers a powerful visual interpretation of its solutions. Each equation in the system can be represented as a line (in a two-variable system) or a plane (in a three-variable system).
For a two-variable system:
If a system of two linear equations has infinitely many solutions, the graphs of the two equations are identical lines. This means they occupy the exact same space on the coordinate plane. Every point on the line represents a solution to the system.
Example:
Consider the system:
x + y = 32x + 2y = 6
If you were to graph these equations, you'd find they are the same line. Multiplying the first equation by 2, we get 2x + 2y = 6, which is identical to the second equation. Therefore, any point on this line, such as (0,3), (1,2), (2,1), (3,0), etc., represents a valid solution.
For a three-variable system:
In a three-variable system, each equation represents a plane in three-dimensional space. A system with infinitely many solutions has planes that either coincide completely (all planes are identical) or intersect in a common line.
Algebraic Identification of Infinitely Many Solutions
While graphical representation provides a visual understanding, algebraic methods are crucial for determining whether a system possesses infinitely many solutions. These methods primarily involve techniques like substitution and elimination.
Using Elimination:
The elimination method involves manipulating the equations to eliminate one variable. If, after performing the elimination, you obtain an equation that is always true (like 0 = 0), this indicates infinitely many solutions.
Example:
Let's consider the system:
x + y = 52x + 2y = 10
Multiply the first equation by -2: -2x - 2y = -10.
Add this to the second equation: (2x + 2y) + (-2x - 2y) = 10 + (-10).
This simplifies to 0 = 0, which is always true. This confirms the system has infinitely many solutions.
Using Substitution:
The substitution method involves solving one equation for one variable and substituting it into the other equation. If this results in an identity (an equation that is always true), the system has infinitely many solutions.
Example:
Consider the system:
y = 2x + 12y = 4x + 2
Substitute the first equation into the second: 2(2x + 1) = 4x + 2.
This simplifies to 4x + 2 = 4x + 2, which is always true, confirming infinitely many solutions.
Row Reduction (Gaussian Elimination):
For larger systems, especially those with more than three variables, row reduction (also known as Gaussian elimination) is a systematic approach. This involves transforming the augmented matrix of the system into row echelon form or reduced row echelon form. Infinitely many solutions are indicated by the presence of free variables – variables that can take on any value without violating the system's equations. This often manifests as a row of zeros in the row-reduced matrix.
Dependent and Independent Equations
The concept of dependent and independent equations is central to understanding systems with infinitely many solutions.
-
Independent equations: Equations that provide unique information. They are not multiples of each other. A system of independent equations will typically have a unique solution or no solution.
-
Dependent equations: Equations that provide redundant information. One equation can be obtained by multiplying the other equation by a constant. Systems with dependent equations often have infinitely many solutions.
Real-World Applications
The concept of infinitely many solutions isn't just a mathematical curiosity; it finds application in various real-world scenarios:
-
Physics: Describing the motion of a particle under constant velocity can yield a system with infinitely many solutions, as the particle's position changes continuously over time.
-
Economics: Linear programming problems, often used in optimization, can sometimes result in systems with infinitely many optimal solutions, representing different ways to achieve the same maximum profit or minimum cost.
-
Computer Graphics: Defining a line or plane in computer graphics often involves systems of equations with infinitely many solutions, representing all the points that lie on that line or plane.
-
Chemistry: Systems of chemical reactions can sometimes lead to situations with infinitely many solution possibilities depending on the stoichiometric ratios and the amounts of reactants available.
Distinguishing Between Infinite Solutions and No Solutions
It's crucial to distinguish between systems with infinitely many solutions and those with no solutions. The key difference lies in the nature of the resulting equations after applying algebraic manipulation:
-
Infinitely many solutions: Leads to an identity (an equation that is always true, like 0 = 0 or x = x).
-
No solutions: Leads to a contradiction (an equation that is always false, like 0 = 1 or x = x + 1).
Advanced Concepts and Extensions
The concepts explored thus far primarily focus on linear systems. However, the idea of infinitely many solutions extends to nonlinear systems as well. For instance, a system of two quadratic equations might intersect at infinitely many points, though the nature of these intersections will be more complex than simple lines.
Furthermore, systems of differential equations can also possess infinitely many solutions, depending on initial conditions and the nature of the equations. These are often solved using techniques beyond the scope of basic algebra.
Conclusion
Understanding systems of equations with infinitely many solutions is a vital aspect of mathematics and its applications. By mastering both the graphical and algebraic methods for identifying such systems, one gains valuable tools for problem-solving in numerous fields. The concepts of dependent equations, row reduction, and the distinction between infinitely many solutions and no solutions are all critical pieces of this puzzle. Remember that while the visual representation is helpful for understanding, algebraic methods are essential for rigorous verification and solving more complex systems. This comprehensive overview provides a strong foundation for further exploration of this fascinating and important topic. Through continued practice and exploration, a deep understanding of this fundamental mathematical concept can be achieved.
Latest Posts
Latest Posts
-
In What Episode Of Bleach Does Ichigo Ask Orihime Out
Jul 13, 2025
-
How Much Is 4 Oz Chocolate Chips
Jul 13, 2025
-
How Many Times Does 9 Go Into 70
Jul 13, 2025
-
4 Pics 1 Word Cheat 8 Letters
Jul 13, 2025
-
220 Kilometers Per Hour To Miles Per Hour
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about Graph Shows A System Of Equations With Infinitely Many Solutions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.