Half Of 1 And 3 4 Cup
Kalali
Jul 02, 2025 · 5 min read
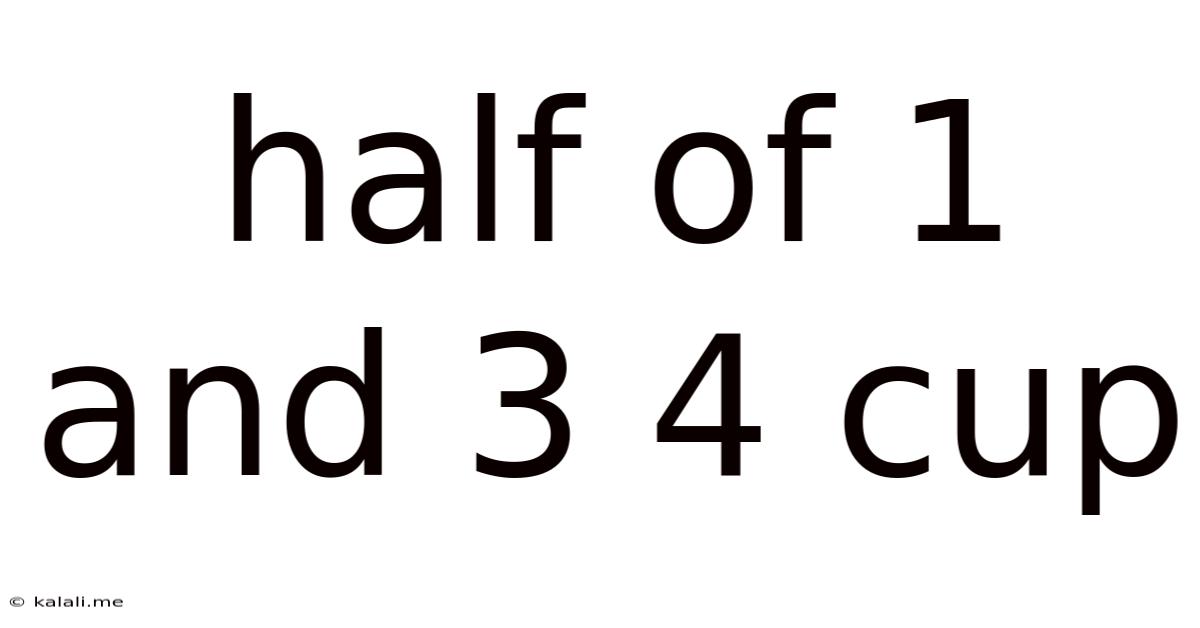
Table of Contents
Decoding "Half of 1 and 3/4 Cup": A Comprehensive Guide to Fraction Calculations in Cooking and Baking
This article delves into the seemingly simple yet often confusing calculation: "half of 1 and 3/4 cups." We'll explore this problem using various methods, offering a clear understanding for both novice cooks and seasoned bakers. Understanding fraction manipulation is crucial for accurate recipe scaling and achieving consistent results in the kitchen. This guide will equip you with the knowledge and confidence to tackle similar fraction problems with ease.
Understanding the Problem: Why Fractions Matter in Cooking
Recipes often require precise ingredient measurements for optimal results. Whether you're halving a recipe for a smaller serving or doubling it for a larger gathering, accurately calculating fractions is essential. Failing to do so can lead to inconsistencies in texture, taste, and overall quality of your culinary creation. The seemingly straightforward task of finding "half of 1 and 3/4 cups" highlights the importance of mastering fractional arithmetic in cooking and baking.
Method 1: Converting to Improper Fractions
This method involves transforming mixed numbers (like 1 and 3/4) into improper fractions for easier calculation. This is often the most efficient approach for more complex fraction problems.
-
Convert the mixed number to an improper fraction: To convert 1 and 3/4 to an improper fraction, we multiply the whole number (1) by the denominator (4), add the numerator (3), and keep the same denominator. This gives us 7/4.
-
Find half of the improper fraction: To find half of 7/4, we multiply it by 1/2: (7/4) * (1/2) = 7/8.
-
The answer: Half of 1 and 3/4 cups is 7/8 cup.
Method 2: Working with Whole Numbers and Fractions Separately
This method breaks down the problem into manageable parts, making it easier to visualize and understand, especially for those less comfortable with improper fractions.
-
Halve the whole number: Half of 1 cup is 1/2 cup.
-
Halve the fraction: Half of 3/4 cup is (3/4) * (1/2) = 3/8 cup.
-
Combine the results: Add the two halves together: 1/2 cup + 3/8 cup. To add these fractions, we need a common denominator (8): (4/8) + (3/8) = 7/8 cup.
-
The answer: Half of 1 and 3/4 cups is 7/8 cup.
Method 3: Decimal Conversion
While less common in traditional baking, converting fractions to decimals can simplify the calculation for some individuals.
-
Convert the mixed number to a decimal: 1 and 3/4 is equal to 1.75 cups.
-
Find half of the decimal: Half of 1.75 cups is 1.75 / 2 = 0.875 cups.
-
Convert back to a fraction (optional): 0.875 can be converted back to a fraction by recognizing that 0.875 is 875/1000, which simplifies to 7/8.
-
The answer: Half of 1 and 3/4 cups is 7/8 cup or 0.875 cup.
Practical Applications and Tips for Cooking and Baking
Understanding how to calculate half of 1 and 3/4 cups has wide-ranging applications in the kitchen. Here are some practical tips:
-
Recipe Scaling: This is crucial when adjusting recipes for different numbers of servings. Knowing how to halve or double fractions ensures accurate ingredient proportions.
-
Ingredient Substitution: Sometimes, you may need to substitute ingredients based on what you have available. Understanding fractions allows for accurate substitutions while maintaining the recipe's integrity.
-
Improvising Recipes: Experienced cooks often adapt recipes based on their preferences and available ingredients. Mastering fraction calculations enables flexible and creative cooking.
-
Using Measuring Cups: While measuring cups are helpful, understanding fractions helps you accurately measure quantities, especially when dealing with smaller amounts. For example, knowing that 7/8 cup is slightly less than a full cup prevents over- or under-measuring.
Beyond the Basics: Handling More Complex Fraction Problems
The principles discussed above can be applied to more complex fraction calculations. For example:
-
Finding 1/3 of 2 and 1/2 cups: Convert 2 and 1/2 to an improper fraction (5/2), then multiply by 1/3: (5/2) * (1/3) = 5/6 cup.
-
Adding and subtracting fractions: Understanding common denominators is essential for adding and subtracting fractions, a common requirement in cooking. For example, adding 1/4 cup and 1/2 cup requires converting 1/2 to 2/4, resulting in a total of 3/4 cup.
-
Multiplying and dividing fractions: These operations are critical for scaling recipes up or down proportionally. Remember that multiplying fractions involves multiplying the numerators and denominators, while dividing fractions involves inverting the second fraction and multiplying.
Conclusion: Mastering Fractions for Culinary Success
Successfully calculating "half of 1 and 3/4 cups" isn't just about getting the right measurement; it's about understanding fundamental mathematical concepts that are crucial for achieving consistent and delicious results in the kitchen. By mastering the methods outlined in this article, you'll gain the confidence to tackle any fractional calculation you encounter in cooking and baking, leading to a more satisfying and rewarding culinary experience. Remember that practice is key – the more you work with fractions, the more comfortable and proficient you'll become. This empowers you to confidently adjust recipes, experiment with new ingredients, and ultimately become a more skilled and creative cook. Embrace the challenge, and enjoy the journey of mastering fractions in your culinary endeavors!
Latest Posts
Latest Posts
-
1 Lb Macaroni Is How Many Cups
Jul 30, 2025
-
How To Hand Sew Two Pieces Of Fabric Together
Jul 30, 2025
-
What Is 1 4 Cup 1 4 Cup
Jul 30, 2025
-
How Many Candy Corn In A Bag
Jul 30, 2025
-
What Percentage Of An Hour Is 15 Minutes
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about Half Of 1 And 3 4 Cup . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.