How Do You Find A Hole In A Rational Function
Kalali
Mar 21, 2025 · 5 min read
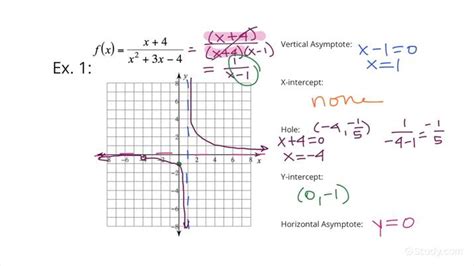
Table of Contents
How Do You Find a Hole in a Rational Function? A Comprehensive Guide
Rational functions, a cornerstone of algebra and calculus, are defined as the ratio of two polynomial functions. Understanding their behavior, particularly identifying discontinuities like holes and vertical asymptotes, is crucial for various applications, from graphing to solving real-world problems. This comprehensive guide delves into the intricacies of locating holes in rational functions, equipping you with the knowledge and techniques to master this essential concept.
Understanding Rational Functions and Their Discontinuities
A rational function takes the general form f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomial functions. The key to finding holes lies in recognizing that discontinuities arise when the denominator, Q(x), equals zero. However, not all zeros of the denominator create a vertical asymptote. A hole (also known as a removable discontinuity) occurs when a factor in the denominator cancels with a corresponding factor in the numerator.
The Difference Between Holes and Vertical Asymptotes
- Holes: Represent points where the function is undefined but could be made continuous by redefining the function at that point. They appear as gaps in the graph.
- Vertical Asymptotes: Represent points where the function approaches positive or negative infinity. They act as barriers that the graph never crosses.
The distinction hinges on whether the factor causing the denominator to be zero also appears in the numerator. If it does, it's a hole; if not, it's a vertical asymptote.
Locating Holes: A Step-by-Step Approach
Finding holes involves a systematic process:
-
Factor the numerator and denominator completely: This is the most critical step. Ensure you've factored each polynomial expression into its prime factors. Look for common factors between the numerator and the denominator. Techniques like factoring by grouping, using the quadratic formula, or recognizing special patterns (difference of squares, sum/difference of cubes) are all valuable tools here.
-
Identify common factors: Once factored, carefully compare the numerator and denominator. Look for any identical factors that appear in both. These common factors are the key to locating holes.
-
Determine the x-coordinate of the hole: Set the common factor(s) equal to zero and solve for x. This gives you the x-coordinate of the hole(s). Remember, each common factor corresponds to a potential hole.
-
Find the y-coordinate of the hole: Substitute the x-coordinate of the hole (obtained in step 3) into the simplified form of the rational function (after canceling the common factors). The resulting value is the y-coordinate. This essentially involves plugging the x-value into the function after removing the factor that created the hole.
-
Express the hole as an ordered pair: Finally, write the hole as an ordered pair (x, y). This clearly defines the location of the hole on the coordinate plane.
Illustrative Examples: Unveiling the Holes
Let's work through a few examples to solidify our understanding:
Example 1:
Find the hole(s) in the rational function: f(x) = (x² - 4) / (x - 2)
-
Factor: The numerator factors as a difference of squares:
(x - 2)(x + 2). The denominator remains(x - 2). -
Identify common factors: The common factor is
(x - 2). -
Determine the x-coordinate: Setting
(x - 2) = 0givesx = 2. -
Find the y-coordinate: Cancel the common factor:
f(x) = (x + 2). Substitutingx = 2givesy = 4. -
Ordered pair: The hole is located at
(2, 4).
Example 2:
Find the hole(s) in the rational function: f(x) = (x³ - 8) / (x² - 4)
-
Factor: The numerator is a difference of cubes:
(x - 2)(x² + 2x + 4). The denominator is a difference of squares:(x - 2)(x + 2). -
Identify common factors: The common factor is
(x - 2). -
Determine the x-coordinate: Setting
(x - 2) = 0givesx = 2. -
Find the y-coordinate: Cancel the common factor and simplify:
f(x) = (x² + 2x + 4) / (x + 2). Substitutex = 2:y = (4 + 4 + 4) / 4 = 3. -
Ordered pair: The hole is located at
(2, 3).
Example 3 (Multiple Holes):
Find the hole(s) in the rational function: f(x) = (x³ - 6x² + 8x) / (x³ - 4x)
-
Factor: Numerator:
x(x² - 6x + 8) = x(x - 2)(x - 4). Denominator:x(x² - 4) = x(x - 2)(x + 2). -
Identify common factors: The common factors are
xand(x-2). -
Determine the x-coordinates: Setting x = 0 gives one x-coordinate. Setting (x-2) = 0 gives another: x = 2.
-
Find the y-coordinates:
- For x = 0: The simplified function after canceling common factors is
(x - 4) / (x + 2). Substituting x = 0 gives y = -2. - For x = 2: The simplified function is
(x - 4) / (x + 2). Substituting x = 2 gives y = -1/2.
- For x = 0: The simplified function after canceling common factors is
-
Ordered pairs: The holes are located at (0, -2) and (2, -1/2).
Advanced Considerations and Applications
The concept of holes extends beyond simple rational functions. It applies to more complex rational expressions and is vital in several areas:
-
Calculus: Identifying holes is crucial for evaluating limits and understanding the behavior of functions near points of discontinuity.
-
Graphing: Accurately plotting rational functions requires identifying and representing holes as open circles on the graph.
-
Real-world modeling: Rational functions model many real-world phenomena; understanding their discontinuities helps interpret these models more accurately. For instance, in physics, a hole could represent a point where a certain quantity is undefined or experiences a sudden change.
Conclusion: Mastering the Art of Finding Holes
Finding holes in rational functions involves a systematic approach that combines factoring, identifying common factors, and careful substitution. By mastering this process, you gain a deeper understanding of rational functions, their behavior, and their applications in various fields. Remember that practice is key to mastering this skill. Work through numerous examples, and gradually increase the complexity of the rational functions you analyze. This detailed guide provides a solid foundation, enabling you to confidently navigate the intricacies of rational functions and their fascinating world of discontinuities.
Latest Posts
Latest Posts
-
How Big Is 54 Inches In Feet
Mar 28, 2025
-
How Hot Is 100 Degrees Celsius
Mar 28, 2025
-
165 Centimeters Is How Many Inches
Mar 28, 2025
-
How Many Grams Is 40 Oz
Mar 28, 2025
-
How Many Grams In 1 4 Ounce
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How Do You Find A Hole In A Rational Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
