How Do You Line Up Decimals When Multiplying
Kalali
Apr 03, 2025 · 5 min read
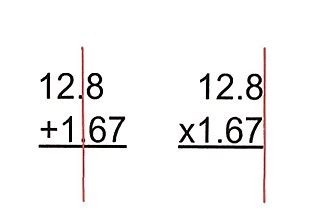
Table of Contents
How Do You Line Up Decimals When Multiplying? A Comprehensive Guide
Multiplying decimals might seem daunting at first, but with a solid understanding of the process, it becomes straightforward. Unlike addition and subtraction, where you line up the decimal points vertically, multiplying decimals requires a different approach. This comprehensive guide will walk you through the steps, explaining the underlying logic and offering various examples to solidify your understanding. We’ll also explore different methods and address common pitfalls.
Understanding the Basics: Why Decimal Point Placement Matters
Before diving into the mechanics of multiplying decimals, let's understand why aligning decimal points during multiplication isn't necessary. The core concept lies in treating decimals as fractions. When you multiply two decimals, you're essentially multiplying two fractions. Consider this example:
0.2 x 0.3 = 2/10 x 3/10 = 6/100 = 0.06
Notice that the number of decimal places in the product (0.06) is the sum of the decimal places in the original numbers (0.2 has one decimal place, and 0.3 has one, totaling two decimal places). This is the key to understanding decimal multiplication.
Step-by-Step Guide to Multiplying Decimals
Here's a breakdown of the process:
-
Ignore the decimal points initially: Treat the numbers as whole numbers and perform the multiplication as you would normally. This is the most crucial step, making the process significantly easier.
-
Count the total number of decimal places: In both numbers being multiplied, add up the total number of digits to the right of the decimal points.
-
Place the decimal point in the product: Starting from the rightmost digit of your answer (the product), count the total number of decimal places you calculated in Step 2. Place the decimal point that many places from the right.
Let's illustrate with an example:
Example 1: Multiplying 2.5 by 1.2
-
Ignore decimal points: Multiply 25 x 12 = 300
-
Count decimal places: 2.5 has one decimal place, and 1.2 has one decimal place, for a total of two decimal places.
-
Place the decimal point: Starting from the rightmost digit in '300', move two places to the left. This gives us 3.00 or simply 3.
Therefore, 2.5 x 1.2 = 3
Example 2: Multiplying 0.04 by 1.5
-
Ignore decimal points: Multiply 4 x 15 = 60
-
Count decimal places: 0.04 has two decimal places, and 1.5 has one decimal place, making a total of three decimal places.
-
Place the decimal point: Starting from the right of '60', count three places to the left. This requires adding a leading zero. We get 0.060 or 0.06.
Therefore, 0.04 x 1.5 = 0.06
Example 3: Multiplying larger decimals with more decimal places
Let's try a more complex example: 12.345 x 3.2
-
Ignore decimal points: Multiply 12345 x 32 = 395040
-
Count decimal places: 12.345 has three decimal places, and 3.2 has one decimal place, totaling four decimal places.
-
Place the decimal point: Count four places from the right in '395040'. This gives us 39.5040 or 39.504
Therefore, 12.345 x 3.2 = 39.504
Multiplying Decimals by Powers of 10
Multiplying decimals by powers of 10 (10, 100, 1000, etc.) is a special case. The decimal point simply moves to the right. The number of places it moves is equal to the number of zeros in the power of 10.
- Multiplying by 10: Move the decimal point one place to the right.
- Multiplying by 100: Move the decimal point two places to the right.
- Multiplying by 1000: Move the decimal point three places to the right.
Example: 2.56 x 100 = 256 (The decimal point moves two places to the right)
Dealing with Zeroes
Zeroes to the right of the last non-zero digit after the decimal point are insignificant and can be dropped. For example, 3.00 is the same as 3. Similarly, 0.060 is the same as 0.06. However, trailing zeros are important in scientific notation and when maintaining precision in calculations.
Common Mistakes to Avoid
- Forgetting to count decimal places: This is the most frequent error. Always carefully count the total number of decimal places in the original numbers.
- Misplacing the decimal point: Double-check your counting and placement of the decimal point in the final answer. It's easy to miscount, especially with larger numbers.
- Not treating the numbers as whole numbers initially: Remember, the ease of the process lies in temporarily ignoring the decimal points.
- Confusion with addition and subtraction: Remember that addition and subtraction require aligning decimal points vertically, while multiplication doesn't.
Alternative Methods and Advanced Concepts
While the step-by-step method described above is the most straightforward, other methods can be helpful for certain situations:
- Using fractions: Converting decimals to fractions can simplify some calculations, particularly when dealing with repeating decimals.
- Scientific notation: For very large or very small numbers, scientific notation offers a more concise and manageable way to perform calculations.
Practice Makes Perfect
The key to mastering decimal multiplication is consistent practice. The more you practice, the more comfortable and accurate you'll become. Start with simple problems and gradually work your way up to more complex ones. Utilize online resources, textbooks, or practice worksheets to enhance your skill.
Remember, understanding the underlying principles – treating decimals as fractions and carefully counting decimal places – is crucial for accurate results. With practice and a clear understanding of the steps involved, you can confidently tackle any decimal multiplication problem. By focusing on these core concepts and avoiding the common pitfalls, you’ll become proficient in this essential mathematical skill. Regular practice, combined with a clear understanding of the rules, will solidify your understanding and help you develop confidence in tackling various decimal multiplication problems. Good luck, and happy calculating!
Latest Posts
Latest Posts
-
What Is 1 1 4 In Mm
Apr 04, 2025
-
14 C Is What In Fahrenheit
Apr 04, 2025
-
How Many Feet In 90 Inches
Apr 04, 2025
-
How Many Inches Is 90 Centimeters
Apr 04, 2025
-
How Much Is 25 Degrees Fahrenheit In Celsius
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How Do You Line Up Decimals When Multiplying . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
