How Do You Multiply Square Root Fractions
Kalali
Apr 02, 2025 · 5 min read
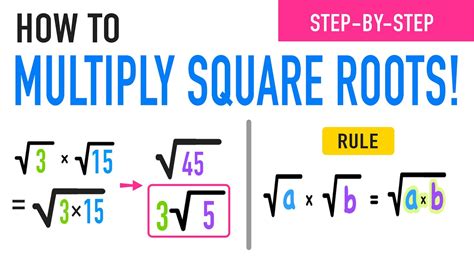
Table of Contents
- How Do You Multiply Square Root Fractions
- Table of Contents
- How Do You Multiply Square Root Fractions? A Comprehensive Guide
- Understanding the Basics: Square Roots and Fractions
- What are Square Roots?
- What are Fractions?
- Combining Square Roots and Fractions: Square Root Fractions
- Multiplying Square Root Fractions: A Step-by-Step Approach
- Advanced Techniques and Examples
- Tips and Tricks for Efficient Calculation
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
How Do You Multiply Square Root Fractions? A Comprehensive Guide
Multiplying square root fractions might seem daunting at first, but with a structured approach and a solid understanding of the underlying principles, it becomes a straightforward process. This comprehensive guide will walk you through the intricacies of multiplying square root fractions, equipping you with the knowledge and skills to tackle various problems with confidence. We'll explore different scenarios, offer practical examples, and provide tips and tricks to streamline your calculations.
Understanding the Basics: Square Roots and Fractions
Before diving into the multiplication of square root fractions, let's refresh our understanding of square roots and fractions individually.
What are Square Roots?
A square root of a number is a value that, when multiplied by itself, gives the original number. For example, the square root of 9 (√9) is 3 because 3 x 3 = 9. Square roots can be integers (whole numbers), decimals, or even irrational numbers (numbers that cannot be expressed as a simple fraction, like π).
What are Fractions?
Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). For instance, ½ represents one part out of two equal parts.
Combining Square Roots and Fractions: Square Root Fractions
A square root fraction is simply a fraction where either the numerator, the denominator, or both contain square roots. For example, √9/4, √16/25, and √2/√3 are all square root fractions.
Multiplying Square Root Fractions: A Step-by-Step Approach
The key to multiplying square root fractions is to apply the fundamental rules of both square roots and fractions systematically. Here's a breakdown of the process:
1. Simplify Individual Square Roots:
Before multiplying, it's crucial to simplify each square root within the fraction as much as possible. This involves finding perfect square factors within the radicand (the number inside the square root symbol).
- Example: Consider the fraction √12/√27.
- √12 can be simplified: √12 = √(4 x 3) = √4 x √3 = 2√3
- √27 can be simplified: √27 = √(9 x 3) = √9 x √3 = 3√3
- Therefore, √12/√27 simplifies to (2√3)/(3√3)
2. Multiply the Numerators and Denominators Separately:
Once the individual square roots are simplified, multiply the numerators together and the denominators together.
- Example (continuing from the previous step): (2√3)/(3√3)
- Multiplying the numerators: 2√3 x 1 = 2√3
- Multiplying the denominators: 3√3 x 1 = 3√3
- Resulting fraction: (2√3)/(3√3)
3. Simplify the Resulting Fraction:
After multiplying, simplify the resulting fraction by canceling out common factors in the numerator and denominator.
- Example (continuing from the previous step): (2√3)/(3√3)
- Notice that √3 is a common factor in both the numerator and denominator.
- Canceling out √3, we get 2/3.
4. Rationalize the Denominator (If Necessary):
If the denominator still contains a square root after simplification, you need to rationalize it. This involves multiplying both the numerator and denominator by the square root in the denominator.
- Example: Let's say we have the fraction √2/√3.
- Multiply both numerator and denominator by √3: (√2 x √3) / (√3 x √3) = √6 / 3
5. Final Simplification:
After rationalization, check for any further simplification possibilities. This might involve simplifying the resulting square root or reducing the fraction.
Advanced Techniques and Examples
Let's delve deeper into more complex scenarios and illustrate the multiplication process with detailed examples.
Example 1: Multiplying Fractions with Multiple Square Roots
Consider the problem: (√8/√2) x (√18/√3)
-
Simplify individual square roots:
- √8 = √(4 x 2) = 2√2
- √2 = √2
- √18 = √(9 x 2) = 3√2
- √3 = √3
-
Rewrite the expression with simplified square roots: (2√2/√2) x (3√2/√3)
-
Multiply numerators and denominators: (2√2 x 3√2) / (√2 x √3) = 6√4 / √6
-
Simplify the resulting square root and fraction: 6(2) / √6 = 12/√6
-
Rationalize the denominator: (12/√6) x (√6/√6) = (12√6)/6 = 2√6
Example 2: Multiplying Fractions with Variables
Let's consider the problem: (√(2x)/√y) x (√(3y)/√(4x))
-
Simplify individual square roots:
- √(2x) = √2x
- √y = √y
- √(3y) = √3y
- √(4x) = 2√x
-
Rewrite the expression: (√2x/√y) x (√3y/2√x)
-
Multiply numerators and denominators: (√2x x √3y) / (√y x 2√x) = √6xy / 2√xy
-
Simplify the resulting square roots: √6 /2
Example 3: Dealing with Negative Numbers Under the Square Root
Remember that the square root of a negative number involves imaginary numbers (denoted by 'i', where i² = -1).
Consider (√(-4)/√9) x (√(-25)/√16)
-
Simplify individual square roots: √(-4) = 2i √9 = 3 √(-25) = 5i √16 = 4
-
Rewrite the expression: (2i/3) x (5i/4)
-
Multiply numerators and denominators: (10i²)/12 = (10(-1))/12 = -10/12 = -5/6
Tips and Tricks for Efficient Calculation
- Master factoring: Proficiency in finding perfect square factors significantly streamlines the simplification process.
- Utilize the properties of square roots: Remember rules like √(a x b) = √a x √b and √(a/b) = √a/√b.
- Practice regularly: Consistent practice strengthens your understanding and improves your speed and accuracy.
- Check your work: Always verify your results to ensure accuracy.
Conclusion
Multiplying square root fractions involves a systematic approach combining the rules of fraction multiplication and square root simplification. By following the steps outlined in this guide, and practicing regularly, you’ll master this mathematical concept. Remember to focus on simplifying individual terms before multiplying, rationalizing the denominator when necessary, and always checking your final answer. With consistent effort and application of the techniques explained above, you'll confidently navigate the world of multiplying square root fractions.
Latest Posts
Latest Posts
-
How Many Ml Is 1 Pint
Apr 08, 2025
-
30 Is What Percent Of 80
Apr 08, 2025
-
What Is 95 Cm In Inches
Apr 08, 2025
-
Briefly Describe How And Where Block Mountains Form
Apr 08, 2025
-
68 Out Of 150 As A Percentage
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about How Do You Multiply Square Root Fractions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.