How Many 3 4 Are In 1
Kalali
Jul 15, 2025 · 5 min read
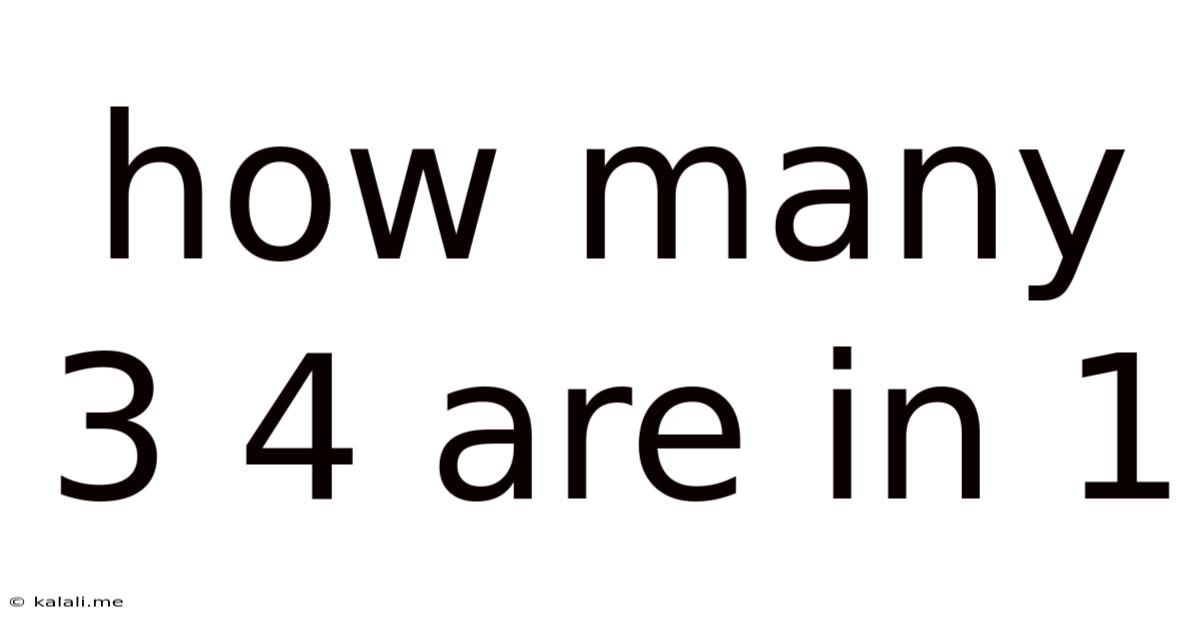
Table of Contents
How Many 3/4s Are in 1? Unpacking Fractions and Division
This seemingly simple question, "How many 3/4s are in 1?", opens the door to a deeper understanding of fractions, division, and their practical applications. While the answer might seem immediately obvious to some, exploring the underlying concepts provides a valuable foundation for more complex mathematical operations. This article will delve into the solution, explaining the process in multiple ways to cater to various learning styles and solidify your understanding of fraction manipulation. We'll also explore real-world scenarios where this type of calculation is relevant.
Understanding the Question: A Foundation in Fractions
The question "How many 3/4s are in 1?" is essentially asking: how many times does 3/4 fit into 1? This translates directly into a division problem: 1 ÷ (3/4). Before we tackle the solution, let's refresh our understanding of key fractional concepts:
- Numerator: The top number of a fraction (e.g., the '3' in 3/4) indicates the number of parts you have.
- Denominator: The bottom number of a fraction (e.g., the '4' in 3/4) indicates the total number of equal parts the whole is divided into.
- Fraction as Division: A fraction can be interpreted as a division problem. 3/4 is the same as 3 divided by 4.
Method 1: The Visual Approach – Using Fraction Bars
Imagine a whole bar representing the number 1. Now, divide this bar into four equal parts. Each part represents 1/4. To represent 3/4, you would shade three of these four parts. The question, "How many 3/4s are in 1?" is visually asking: how many sets of three shaded parts can you fit into the entire bar?
You can clearly see that only one complete set of three shaded parts (representing 3/4) fits entirely within the whole bar. Therefore, there is one 3/4 in 1. However, there's a remaining 1/4. While this method provides a great visual understanding, it’s less effective for larger or more complex fractions.
Method 2: Inverting and Multiplying – The Standard Algorithmic Approach
The most common method to solve this type of division problem involving fractions is to invert (flip) the second fraction and then multiply. This is based on the rule that dividing by a fraction is the same as multiplying by its reciprocal.
1 ÷ (3/4) = 1 × (4/3) = 4/3
This result, 4/3, is an improper fraction (where the numerator is larger than the denominator). To convert it to a mixed number (a whole number and a fraction), we perform the division:
4 ÷ 3 = 1 with a remainder of 1.
Therefore, 4/3 can be written as 1 1/3. This means there is one whole 3/4 in 1, and an additional 1/3 of a 3/4 remaining.
Method 3: Understanding the Remainder
The result 1 1/3 highlights an important point: the initial calculation only tells us how many complete sets of 3/4 are in 1. It doesn't directly answer "how many 3/4s are in 1" if we allow for partial 3/4s. To understand this, let's look at the remainder:
We have 1/3 left over. This represents 1/3 of a 3/4. To find out the fractional part of a 3/4, we multiply 1/3 by 3/4:
(1/3) × (3/4) = 1/4
This means the remaining part is equivalent to 1/4 of the original whole.
Method 4: Solving Using Decimal Equivalents
Converting fractions to decimals can sometimes simplify the process. Let's convert 3/4 to a decimal:
3 ÷ 4 = 0.75
Now, we divide 1 by 0.75:
1 ÷ 0.75 = 1.333...
This decimal result (1.333...) confirms our previous findings. The '1' represents one whole 3/4, and the '.333...' represents the remaining fraction, which is approximately 1/3 of a 3/4 or 1/4 of the whole.
Real-World Applications: Where This Calculation Matters
This seemingly basic calculation has practical applications across various fields:
-
Cooking and Baking: Recipes often require fractional measurements. Understanding how many portions of a specific ingredient are needed from a larger quantity (1 whole unit) is crucial for accurate measurements. For example, if a recipe calls for 3/4 cup of sugar and you only have 1 cup, you know you have enough and can adjust other elements accordingly.
-
Construction and Engineering: Precision is paramount in construction and engineering. Calculations involving fractions are essential for accurate measurements and material estimations. For instance, determining the number of 3/4-inch tiles needed to cover a 1-inch space is directly related to this principle.
-
Finance: When working with percentages or proportions, understanding fraction division is necessary. For example, calculating how many payments of 3/4 of a debt are required to repay a total loan can be solved similarly.
-
Data Analysis: Statistical analysis often involves manipulating fractions and proportions. Understanding the relationship between fractions and division is fundamental for interpreting and reporting findings.
-
Time Management: Dividing a certain amount of time into fractional units is a common everyday task. For example, figuring out how many 45-minute (3/4 of an hour) blocks are in a one-hour timeframe is equivalent to our original problem.
Conclusion: Mastering Fraction Division
The question of how many 3/4s are in 1 might seem trivial at first glance. However, exploring its solution through various methods illuminates the underlying principles of fraction division and strengthens mathematical understanding. By mastering these techniques – using visual representations, inverting and multiplying, analyzing remainders, and employing decimal equivalents – you build a solid foundation for tackling more complex problems in mathematics and its countless real-world applications. This understanding extends far beyond simple calculations, becoming a valuable tool for problem-solving across diverse fields. Remember, a strong grasp of fractions is essential for success in many areas of life and work.
Latest Posts
Latest Posts
-
If Your 31 What Year Were You Born
Jul 15, 2025
-
How Many Tenths Are In An Inch
Jul 15, 2025
-
Which Word Has The Most Positive Connotation
Jul 15, 2025
-
How Do I Send An Evite Reminder
Jul 15, 2025
-
When Performing A Self Rescue When Should You Swim To Shore
Jul 15, 2025
Related Post
Thank you for visiting our website which covers about How Many 3 4 Are In 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.