How Many Lines Of Symmetry Does A Rectangle Have
Kalali
Apr 04, 2025 · 6 min read
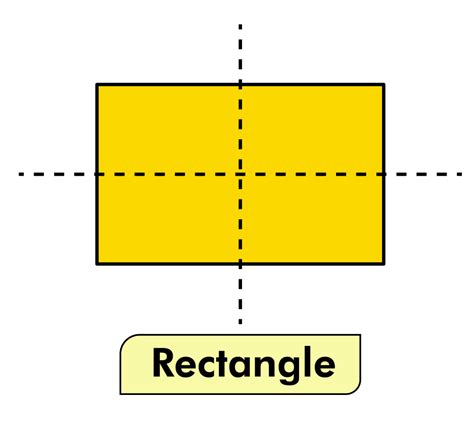
Table of Contents
How Many Lines of Symmetry Does a Rectangle Have? A Comprehensive Guide
Symmetry, a fundamental concept in geometry and art, refers to a balanced and proportionate arrangement of parts. Understanding lines of symmetry is crucial in various fields, from architecture and design to mathematics and computer graphics. This article delves deep into the concept of lines of symmetry, focusing specifically on rectangles and exploring the different types of symmetry they possess. We'll unravel the mathematical underpinnings, explore practical applications, and tackle common misconceptions.
Defining Lines of Symmetry
A line of symmetry, also known as a line of reflection or an axis of symmetry, is a line that divides a shape into two identical halves that are mirror images of each other. If you were to fold the shape along the line of symmetry, both halves would perfectly overlap. This concept is central to understanding the symmetry of geometric shapes, including rectangles.
The Rectangle: A Closer Look
A rectangle is a quadrilateral (a four-sided polygon) with four right angles (90-degree angles). Its opposite sides are equal in length and parallel to each other. This seemingly simple shape exhibits interesting properties concerning its lines of symmetry.
Types of Symmetry
Rectangles possess two distinct types of symmetry:
-
Reflectional Symmetry: This is the most common type of symmetry associated with lines of symmetry. A rectangle has reflectional symmetry across two lines: one that runs horizontally through the center, and another that runs vertically through the center.
-
Rotational Symmetry: A shape has rotational symmetry if it can be rotated less than 360 degrees about a central point and still look exactly the same. Rectangles possess rotational symmetry of order 2. This means that they look identical after a rotation of 180 degrees about their center. A full 360-degree rotation would, of course, also result in the same appearance, but this isn't considered a unique rotational symmetry.
How Many Lines of Symmetry Does a Rectangle Have?
The answer, based on the definition of lines of symmetry and the properties of a rectangle, is two. A rectangle possesses two lines of symmetry:
-
A horizontal line of symmetry: This line passes through the midpoints of the top and bottom sides of the rectangle. Folding the rectangle along this line results in perfect overlap of the two halves.
-
A vertical line of symmetry: This line passes through the midpoints of the left and right sides of the rectangle. Similar to the horizontal line, folding along this line creates a perfect mirror image.
Understanding the Difference Between Rectangles and Squares
A square is a special type of rectangle where all four sides are equal in length. This additional property leads to a difference in the number of lines of symmetry. While a rectangle has two lines of symmetry, a square has four lines of symmetry: two diagonals in addition to the horizontal and vertical lines. The diagonals of a square act as lines of reflection, dividing the shape into two congruent triangles. This highlights the relationship between the properties of a shape and its symmetry.
Applications of Symmetry in Rectangles
The presence of lines of symmetry in rectangles has significant implications across various fields:
-
Architecture and Design: Many buildings and structures incorporate rectangular elements due to their inherent stability and aesthetic appeal. The symmetrical nature of rectangles contributes to the visual balance and harmony of these designs. Think of the windows, doors, and overall structure of many buildings.
-
Graphic Design and Art: Rectangles provide a stable framework for creating visually balanced compositions. In graphic design, logos, posters, and website layouts often utilize rectangles, taking advantage of their symmetrical properties to create visually appealing designs.
-
Engineering and Manufacturing: Rectangular components are commonly used in engineering and manufacturing because their symmetry simplifies design and manufacturing processes. The symmetrical nature allows for easier assembly and more predictable performance.
-
Computer Graphics: In computer graphics, rectangles and their symmetrical properties are fundamental building blocks for creating images and animations. They're often used as basic primitives for representing objects and defining areas on a screen.
Misconceptions About Lines of Symmetry in Rectangles
A common misconception is that any line that divides a rectangle into two equal areas is a line of symmetry. This is incorrect. A line of symmetry must not only divide the shape into two equal areas but also create two halves that are mirror images of each other. A line that divides a rectangle into two equal areas but doesn't create mirror images is not a line of symmetry.
Exploring Further: Irregular Rectangles and their Symmetry
While the standard concept of a rectangle usually refers to a shape with perfectly right angles, let's consider the possibility of a slightly irregular rectangle. For example, imagine a rectangle where one pair of opposite sides is slightly longer or shorter than the other. Does this change the number of lines of symmetry?
The answer is no. Even with this irregularity, it will still only possess two lines of symmetry - a horizontal and a vertical line passing through the midpoints of the opposite sides. The principle remains consistent: the lines must create perfect mirror images of the two halves. The irregularity may affect the overall visual balance, but it doesn't alter the fundamental symmetry.
Beyond Rectangles: Symmetry in Other Shapes
Exploring the symmetry of other geometric shapes is a natural extension of understanding rectangular symmetry. Let's briefly touch on a few examples:
-
Squares: As mentioned earlier, squares possess four lines of symmetry: two diagonals and two lines that bisect the opposite sides. They also have rotational symmetry of order 4.
-
Circles: Circles exhibit infinite lines of symmetry, as any diameter acts as a line of symmetry. They also have infinite rotational symmetry.
-
Triangles: The number of lines of symmetry in a triangle depends on its type. An equilateral triangle (all sides equal) has three lines of symmetry, one from each vertex to the midpoint of the opposite side. An isosceles triangle (two sides equal) has one line of symmetry, and a scalene triangle (no sides equal) has none.
Conclusion: The Significance of Symmetry
Understanding the lines of symmetry in a rectangle, and other shapes for that matter, is more than just a mathematical exercise. It's a fundamental concept with wide-reaching applications in diverse fields. From the design of everyday objects to the creation of complex architectural structures, the principles of symmetry contribute to visual appeal, structural integrity, and functional efficiency. This comprehensive guide has explored the intricacies of rectangular symmetry, clarified common misconceptions, and provided a foundation for further exploration of symmetry in various geometric shapes. Remember that the key to identifying lines of symmetry is the creation of perfect mirror images upon reflection along the line. Understanding this crucial aspect provides a solid basis for appreciating and applying the concept of symmetry in many different contexts.
Latest Posts
Latest Posts
-
Does Gold Set Off Metal Detectors
Apr 10, 2025
-
How Long Is 75 Cm In Inches
Apr 10, 2025
-
What Is 1 7 As A Decimal
Apr 10, 2025
-
Starch And Glycogen Are Examples Of
Apr 10, 2025
-
4 Is What Percent Of 25
Apr 10, 2025
Related Post
Thank you for visiting our website which covers about How Many Lines Of Symmetry Does A Rectangle Have . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.