How Many Sides Does A Quadrilateral
Kalali
Mar 26, 2025 · 5 min read
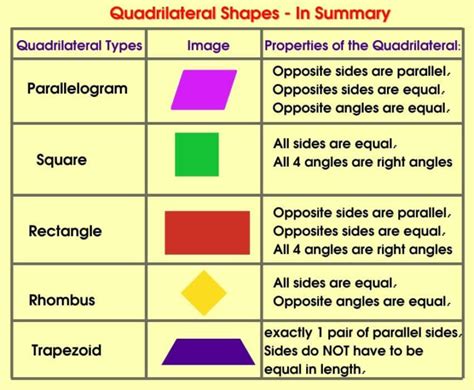
Table of Contents
How Many Sides Does a Quadrilateral Have? A Deep Dive into Quadrilaterals
The question, "How many sides does a quadrilateral have?" might seem incredibly simple at first glance. The answer, of course, is four. However, the seemingly straightforward nature of this question belies a rich world of geometric properties, classifications, and applications that make quadrilaterals a fascinating subject in mathematics. This article delves into the intricacies of quadrilaterals, exploring their defining characteristics, different types, and their significance in various fields. We’ll move beyond the simple answer and uncover the fascinating details hidden within this fundamental geometric shape.
Understanding the Basics: Defining a Quadrilateral
Before we delve into the specifics of different types of quadrilaterals, let's solidify our understanding of the fundamental definition. A quadrilateral is a polygon with four sides, four angles, and four vertices. The word "quadrilateral" itself is a combination of "quad," meaning four, and "lateral," referring to sides. This simple definition lays the groundwork for a diverse family of shapes, each with its own unique properties.
Key Properties of Quadrilaterals
Several key properties characterize all quadrilaterals, regardless of their specific type. These include:
-
Sum of Interior Angles: The sum of the interior angles of any quadrilateral always equals 360 degrees. This is a crucial property used in various geometric proofs and calculations.
-
Diagonals: All quadrilaterals possess two diagonals, which are line segments connecting opposite vertices. The lengths and properties of these diagonals vary depending on the type of quadrilateral.
-
Area Calculation: The formula for calculating the area of a quadrilateral depends on the specific type of quadrilateral. We'll explore the area formulas for various quadrilaterals later in this article.
-
Perimeter: The perimeter of a quadrilateral is simply the sum of the lengths of its four sides.
Classifying Quadrilaterals: A Hierarchy of Shapes
The beauty of quadrilaterals lies in their diverse classifications. Based on their properties – such as the lengths of their sides, the measure of their angles, and the properties of their diagonals – quadrilaterals can be categorized into various sub-types. This hierarchy provides a structured way to understand the relationships between different quadrilateral shapes.
1. Parallelograms: Sides and Angles Working in Harmony
A parallelogram is a quadrilateral where both pairs of opposite sides are parallel and equal in length. This leads to several significant properties:
-
Opposite Angles are Equal: Opposite angles in a parallelogram are congruent (equal in measure).
-
Consecutive Angles are Supplementary: Consecutive angles (angles that share a side) are supplementary, meaning their sum is 180 degrees.
-
Diagonals Bisect Each Other: The diagonals of a parallelogram intersect at their midpoints.
Several specific types of parallelograms fall under this broader category:
-
Rectangles: Parallelograms with four right angles (90-degree angles).
-
Rhombuses (or Rhombi): Parallelograms with four sides of equal length.
-
Squares: Parallelograms that are both rectangles and rhombuses – possessing four right angles and four sides of equal length.
2. Trapezoids: A Single Parallel Pair
A trapezoid (or trapezium in some regions) is a quadrilateral with at least one pair of parallel sides. These parallel sides are called bases, and the other two sides are called legs.
- Isosceles Trapezoids: These trapezoids have legs of equal length, resulting in equal base angles.
3. Kites: Two Pairs of Adjacent Equal Sides
A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. Unlike parallelograms, the opposite sides of a kite are not necessarily parallel or equal. Kites possess a unique property: their diagonals are perpendicular to each other.
4. Irregular Quadrilaterals: The Wild Cards
Any quadrilateral that doesn't fit into the above categories is considered an irregular quadrilateral. These shapes lack specific properties like parallel sides or equal angles, making them the most diverse group within the quadrilateral family.
The Significance of Quadrilaterals: Applications in Real Life
Quadrilaterals are not just abstract geometric shapes; they have numerous practical applications in various fields:
-
Architecture and Construction: Buildings, bridges, and other structures often utilize quadrilateral shapes for their stability and structural integrity. Understanding the properties of different quadrilaterals is crucial for engineers and architects to design safe and efficient structures. Rectangles and squares, in particular, are fundamental building blocks in architectural design.
-
Art and Design: Quadrilaterals are frequently employed in art and design to create balance, symmetry, and visual appeal. From paintings to graphic design to textile patterns, quadrilaterals contribute to the aesthetic qualities of many artistic works.
-
Cartography and Surveying: Quadrilaterals play a crucial role in surveying and mapping. Methods like triangulation, which involve creating networks of triangles from quadrilateral measurements, are used to determine distances and coordinates.
-
Computer Graphics and Programming: Understanding quadrilaterals is essential in computer graphics and programming. These shapes are used to represent surfaces, textures, and objects in 3D modeling and animation.
-
Everyday Objects: Numerous everyday objects are based on quadrilateral shapes. Think of doors, windows, tables, books, and countless other items that utilize rectangles and squares as their fundamental forms.
Exploring Advanced Concepts: Area Formulas and Geometric Proofs
The study of quadrilaterals extends beyond their basic definitions and classifications. Advanced concepts, such as area calculation and geometric proofs, deepen our understanding of these shapes.
Area Formulas for Various Quadrilaterals
Calculating the area of a quadrilateral varies depending on its type. Here are some key formulas:
-
Rectangle: Area = length × width
-
Square: Area = side²
-
Parallelogram: Area = base × height
-
Trapezoid: Area = ½(base1 + base2) × height
-
Kite: Area = ½ × diagonal1 × diagonal2
For irregular quadrilaterals, more complex methods, such as dividing the quadrilateral into triangles, might be necessary to calculate the area.
Geometric Proofs Involving Quadrilaterals
Geometric proofs utilizing quadrilaterals often involve proving the congruence or similarity of triangles formed within the quadrilateral, employing theorems like the Pythagorean theorem or the properties of parallel lines. These proofs are essential for solidifying understanding and demonstrating the relationships between different quadrilaterals.
Conclusion: Beyond the Four Sides
While the simple answer to "How many sides does a quadrilateral have?" is four, the journey of understanding quadrilaterals extends far beyond this basic fact. The diverse types of quadrilaterals, their unique properties, and their widespread applications demonstrate the profound significance of these seemingly simple shapes in mathematics and numerous practical fields. By exploring their intricacies, we gain a deeper appreciation for the elegant world of geometry and its powerful influence on our understanding of the world around us. From the simple rectangle to the more complex irregular quadrilateral, each shape holds a unique place within the fascinating family of four-sided polygons.
Latest Posts
Latest Posts
-
The Is The Fundamental Unit Of Life
Mar 29, 2025
-
How Many Cm Is 4 6
Mar 29, 2025
-
100 Of 500 Is What Percent
Mar 29, 2025
-
How Many Grams Is A 8th Of An Ounce
Mar 29, 2025
-
How Many Feet Is 66 5 Inches
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides Does A Quadrilateral . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
