How Many Sides Does A Square Has
Kalali
Mar 26, 2025 · 5 min read
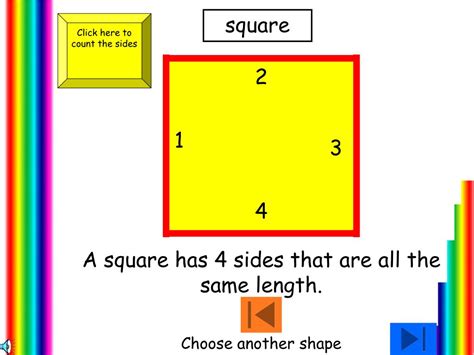
Table of Contents
How Many Sides Does a Square Have? A Deep Dive into Geometry
The seemingly simple question, "How many sides does a square have?" opens a door to a fascinating exploration of geometry, mathematics, and the very nature of shapes. While the answer is immediately apparent to most – four – delving deeper reveals a rich tapestry of concepts, properties, and related shapes that are crucial to understanding the fundamentals of geometry. This comprehensive guide will not only answer the titular question definitively but also explore the characteristics of squares, their relationships to other polygons, and their applications in various fields.
Understanding the Basics: Defining a Square
Before jumping into the intricacies, let's solidify our understanding of what constitutes a square. A square, in its simplest definition, is a two-dimensional shape with four sides of equal length and four right angles (90-degree angles). This simple definition encapsulates several key properties:
- Equilateral: All four sides are of equal length. This is a defining characteristic that distinguishes it from other quadrilaterals.
- Equiangular: All four interior angles are equal and measure 90 degrees each. This right-angled nature is another crucial property.
- Closed Shape: The four sides connect to form a closed figure, enclosing a specific area.
- Regular Polygon: A square is a special case of a polygon, specifically a regular polygon, meaning it has equal sides and equal angles.
The fact that a square possesses four sides is fundamental to its very definition. Without these four equal sides, it would cease to be a square and would instead fall into the category of other quadrilaterals like rectangles, rhombuses, or parallelograms, each with their own unique characteristics.
Exploring Related Shapes: Expanding the Geometric Landscape
Understanding the square's relationship to other shapes provides further insight into its properties. Let's explore some key connections:
1. Quadrilaterals: The Broader Family
Squares belong to a larger family of shapes known as quadrilaterals. Quadrilaterals are polygons with four sides. Squares share some properties with other quadrilaterals, but also possess unique characteristics that set them apart:
- Rectangles: Squares are special types of rectangles. Rectangles have four right angles but their sides don't necessarily have equal lengths. A square is a rectangle with all sides equal.
- Rhombuses: Squares are also special types of rhombuses. Rhombuses have four equal sides, but their angles aren't necessarily right angles. A square is a rhombus with four right angles.
- Parallelograms: Squares are also parallelograms. Parallelograms have opposite sides parallel and equal in length. Squares fulfill these conditions, in addition to having right angles and equal sides.
This hierarchical relationship highlights the specific properties that make a square a square. It’s not just a quadrilateral; it’s a specific type of rectangle, rhombus, and parallelogram.
2. Polygons: Beyond Four Sides
Squares are part of a broader group of shapes called polygons. Polygons are closed shapes with three or more straight sides. Squares, with their four sides, represent a simple yet fundamental polygon. Exploring other polygons helps contextualize the square's place within the larger geometric landscape:
- Triangles: Three-sided polygons.
- Pentagons: Five-sided polygons.
- Hexagons: Six-sided polygons.
- And so on... The number of sides can increase indefinitely.
Understanding this broader classification underscores the importance of the number of sides in defining a shape's geometric properties.
Applications of Squares: From Art to Architecture
The seemingly simple four-sided square finds incredible utility across diverse fields:
1. Architecture and Engineering
Squares and square-based structures are ubiquitous in architecture and engineering. Their stability and ease of construction make them ideal for building foundations, rooms, and even entire buildings. The strength of a square shape means that it can distribute weight evenly, making it a reliable building block for sturdy structures.
2. Art and Design
Squares feature prominently in art and design. Their symmetrical nature lends itself to creating balance and harmony in compositions. Artists and designers leverage the square’s properties to create visually appealing and well-proportioned works. From the square canvases of paintings to the grid-like patterns in textiles, the square's presence is undeniable.
3. Games and Puzzles
Many games and puzzles utilize square grids as their foundation. Chessboards, Sudoku grids, and countless other games depend on the structure and properties of squares for their gameplay mechanics. The regularity and simplicity of the square make it an ideal platform for structuring interactive experiences.
Advanced Concepts: Exploring Deeper into Geometry
Delving deeper into geometry reveals more complex relationships involving squares:
1. Area and Perimeter
Calculating the area and perimeter of a square is a foundational concept in geometry. The area (A) is found by squaring the length of one side (s): A = s². The perimeter (P) is found by multiplying the side length by four: P = 4s. These simple formulas showcase the direct relationship between the side length and the overall dimensions of the square.
2. Diagonal Relationships
The diagonal of a square divides it into two congruent right-angled triangles. Using the Pythagorean theorem (a² + b² = c²), we can calculate the length of the diagonal (d) based on the side length (s): d = s√2. This demonstrates the powerful interplay between the sides and diagonal within the square.
3. Tessellations and Tilings
Squares perfectly tessellate, meaning they can be arranged to cover a plane without any gaps or overlaps. This property is utilized extensively in tiling floors, designing patterns, and even in the structure of some natural formations. The ability of squares to create a seamless and repetitive pattern highlights their unique geometric properties.
Conclusion: The Significance of Four Sides
The question, "How many sides does a square have?" might seem trivial at first glance. However, a deeper exploration reveals the rich mathematical and geometrical significance of this seemingly simple shape. The four sides of a square are not just a defining characteristic; they are the foundation upon which numerous properties, relationships, and applications are built. From its fundamental place in geometry to its widespread use in art, architecture, and beyond, the square stands as a testament to the power of simple shapes to hold profound significance. Understanding the square, and its four sides, provides a crucial stepping stone to mastering the broader concepts of geometry and mathematics.
Latest Posts
Latest Posts
-
How Much Is 80 Inches In Feet
Mar 29, 2025
-
What Is A 15 Out Of 18
Mar 29, 2025
-
Los Hongos Producen Su Propio Alimento
Mar 29, 2025
-
How Many Feet Is 126 Inches
Mar 29, 2025
-
What Percent Is 12 Of 15
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about How Many Sides Does A Square Has . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
