How Much Is 20 Of 100
Kalali
Mar 21, 2025 · 5 min read
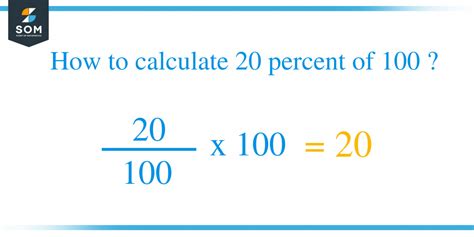
Table of Contents
How Much is 20 of 100? A Deep Dive into Percentages and Fractions
The seemingly simple question, "How much is 20 of 100?" opens a door to a fascinating world of mathematics, specifically percentages and fractions. While the answer might seem immediately obvious to some, understanding the underlying concepts and their applications is crucial for navigating various aspects of life, from everyday budgeting to complex financial analysis. This comprehensive guide will explore this question in detail, covering its basic answer, practical applications, and the broader mathematical principles involved.
The Simple Answer: 20%
The most straightforward answer to "How much is 20 of 100?" is 20%. This is because percentages are essentially fractions expressed as parts of 100. The phrase "20 of 100" directly translates to the fraction 20/100, which simplifies to 1/5. Multiplying this fraction by 100% gives us 20%.
Understanding Percentages
Percentages are a powerful tool for expressing proportions and ratios. They provide a standardized way to compare different quantities and make calculations easier to understand. The term "percent" itself originates from the Latin phrase "per centum," meaning "out of one hundred." This inherent connection to 100 is the key to understanding percentage calculations.
Calculating Percentages
Calculating percentages involves several key steps:
-
Identify the whole: This is the total amount you're considering. In our example, the whole is 100.
-
Identify the part: This is the portion of the whole you're interested in. In our example, the part is 20.
-
Divide the part by the whole: This gives you a decimal representation of the proportion. In this case, 20/100 = 0.2.
-
Multiply the result by 100: This converts the decimal to a percentage. 0.2 * 100 = 20%.
Understanding Fractions
Fractions are another fundamental concept in mathematics, closely related to percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). In our example, "20 of 100" is represented by the fraction 20/100.
Simplifying Fractions
Fractions can often be simplified by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by it. The GCD of 20 and 100 is 20. Dividing both the numerator and denominator by 20 simplifies the fraction 20/100 to 1/5. This means that 20 out of 100 is equivalent to 1 out of 5.
Practical Applications of Percentages and Fractions
The concepts of percentages and fractions are ubiquitous in everyday life. Here are some examples:
1. Finance and Budgeting:
- Interest rates: Interest on loans and savings accounts is expressed as a percentage. Understanding percentages is crucial for calculating interest earned or paid.
- Discounts and sales: Sales and discounts are often advertised as percentages off the original price. Knowing how to calculate these percentages is vital for making informed purchasing decisions.
- Tax calculations: Taxes are typically expressed as a percentage of income or the value of goods and services.
- Investment returns: Investment returns are expressed as percentages, allowing investors to compare the performance of different investments.
2. Science and Statistics:
- Data analysis: Percentages are used extensively in statistics to represent proportions and probabilities. For example, expressing survey results as percentages makes it easier to understand trends and patterns.
- Scientific measurements: Percentages are used to express error margins and variations in scientific measurements.
3. Everyday Life:
- Cooking and baking: Recipes often specify ingredients as proportions or percentages of the total weight or volume.
- Shopping: Comparing prices and values requires understanding percentages and discounts.
- Tip calculations: Calculating tips in restaurants often involves calculating a percentage of the bill.
Beyond the Basics: Advanced Concepts
While the basic calculation of "20 of 100" is straightforward, understanding the underlying mathematical concepts allows for more complex calculations and problem-solving.
Percentage Increase and Decrease
Calculating percentage increase or decrease involves comparing two values and determining the change as a percentage of the original value. For example, if a price increases from $100 to $120, the percentage increase is calculated as follows:
- Find the difference: $120 - $100 = $20
- Divide the difference by the original value: $20 / $100 = 0.2
- Multiply by 100 to express as a percentage: 0.2 * 100 = 20%
Similarly, percentage decrease can be calculated using the same method.
Compound Interest
Compound interest is the interest earned on both the principal amount and accumulated interest from previous periods. It's a powerful concept used in investments and loans. Understanding compound interest requires a solid grasp of percentages and exponential growth.
Ratios and Proportions
Percentages are closely linked to ratios and proportions. A ratio is a comparison of two quantities, often expressed as a fraction. A proportion is a statement that two ratios are equal. Solving problems involving ratios and proportions requires understanding how to manipulate fractions and percentages.
Conclusion: The Power of Understanding Percentages and Fractions
The seemingly simple question, "How much is 20 of 100?" serves as a gateway to a broader understanding of percentages and fractions – fundamental mathematical concepts with wide-ranging applications. From managing personal finances to understanding complex scientific data, mastering these concepts is crucial for navigating the world effectively. This guide has explored the basic calculation, practical applications, and advanced concepts related to percentages and fractions, emphasizing their importance in various aspects of life. By understanding these concepts thoroughly, individuals can make informed decisions, solve problems efficiently, and gain a deeper appreciation for the power of mathematics in everyday life. Remember that consistent practice and application are key to solidifying your understanding and building confidence in working with percentages and fractions.
Latest Posts
Latest Posts
-
Cuanto Son 100 Pies A Metros
Mar 28, 2025
-
How Many Ounces Of Sour Cream Are In A Cup
Mar 28, 2025
-
Does A Catfish Have A Backbone
Mar 28, 2025
-
How Many Feet Are In 42 Inches
Mar 28, 2025
-
How Many Acres Is A Square Mile
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about How Much Is 20 Of 100 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
