How To Find A Hole In A Rational Function
Kalali
Apr 03, 2025 · 5 min read
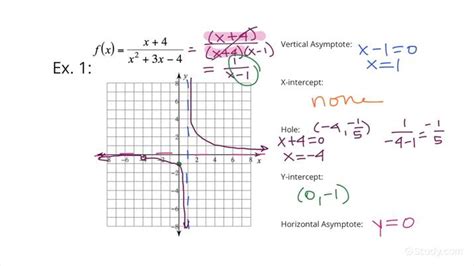
Table of Contents
How to Find Holes in a Rational Function
Rational functions, the ratio of two polynomial functions, often exhibit fascinating behavior. One such feature is the presence of "holes," points where the function appears undefined but can be "filled" by assigning a specific value. Understanding how to identify these holes is crucial for accurately graphing and analyzing rational functions. This comprehensive guide delves into the intricacies of finding holes in rational functions, providing step-by-step instructions and illustrative examples.
Understanding Rational Functions and Their Holes
A rational function is defined as f(x) = p(x) / q(x), where p(x) and q(x) are polynomial functions, and q(x) is not the zero polynomial (otherwise, the function would be undefined everywhere). A hole, also known as a removable discontinuity, occurs at a point x = a when both p(x) and q(x) share a common factor of (x - a). This common factor creates a zero in both the numerator and denominator at x = a, resulting in an indeterminate form of 0/0. The hole is "removable" because we can algebraically simplify the function to eliminate the common factor, thus defining the function's value at x = a.
Steps to Find Holes in a Rational Function
Finding holes involves a systematic approach:
1. Factor Both the Numerator and the Denominator:
This is the foundational step. Completely factor both p(x) and q(x) to identify any common factors. This often involves techniques like factoring quadratics, difference of squares, or grouping.
Example: Consider the function f(x) = (x² - 4) / (x² - x - 2).
Factoring, we get:
f(x) = (x - 2)(x + 2) / (x - 2)(x + 1)
2. Identify Common Factors:
Once factored, look for identical factors in both the numerator and the denominator. These are the key indicators of holes.
In our example, (x - 2) is a common factor.
3. Cancel Common Factors (BUT Don't Forget About Them!):
Cancel out the common factor(s) from both the numerator and the denominator. This simplification gives the simplified form of the rational function, which is crucial for understanding the function's behavior.
Simplified function: f(x) = (x + 2) / (x + 1)
4. Determine the x-coordinate of the Hole:
The x-coordinate of the hole is the value of x that makes the canceled common factor equal to zero.
In our example, setting (x - 2) = 0 gives us x = 2. Therefore, the hole is located at x = 2.
5. Determine the y-coordinate of the Hole:
Substitute the x-coordinate of the hole into the simplified rational function to find the y-coordinate. This gives the y-value the function would have had if the hole didn't exist.
Substituting x = 2 into f(x) = (x + 2) / (x + 1), we get:
f(2) = (2 + 2) / (2 + 1) = 4/3
Therefore, the coordinates of the hole are (2, 4/3).
6. Write the Complete Description:
The final step is to clearly state the location of the hole. For example: "There is a hole in the graph of the function at the point (2, 4/3)."
Advanced Scenarios and Considerations
While the above steps handle most cases, some scenarios require additional attention:
Multiple Holes: A rational function can have more than one hole. If there are multiple common factors, repeat steps 3-5 for each common factor.
Example: f(x) = (x² - 5x + 6) / (x³ - 3x² - 4x + 12)
Factoring gives: f(x) = (x - 2)(x - 3) / (x - 2)(x - 3)(x + 2)
There are holes at x = 2 and x = 3. The simplified function is f(x) = 1/(x + 2).
Substituting x = 2 gives f(2) = 1/4, and substituting x = 3 gives f(3) = 1/5. Holes are at (2, 1/4) and (3, 1/5).
Higher-Degree Polynomials: Factoring higher-degree polynomials can be challenging. Techniques like synthetic division, the rational root theorem, or numerical methods might be necessary. Remember to factor completely to find all common factors.
Irreducible Quadratic Factors: Sometimes, the numerator and denominator might share a quadratic factor that cannot be factored further using real numbers. While the factor can't be canceled directly, it still indicates a behavior akin to a hole, albeit a more complex one involving complex numbers.
Graphing Rational Functions with Holes
Graphing rational functions with holes requires careful attention to detail. You'll need to:
-
Plot the hole: Mark the hole's coordinates on the graph using an open circle. This visually represents the discontinuity.
-
Graph the simplified function: Graph the simplified rational function as you would any other rational function, considering asymptotes (vertical, horizontal, oblique), intercepts, and the overall behavior. The graph of the simplified function will accurately represent the behavior of the original function except at the location of the hole.
-
Understand the behavior around the hole: The graph will approach but never actually reach the y-coordinate of the hole at the x-coordinate of the hole. This behavior shows that the point is a removable discontinuity.
The Importance of Understanding Holes
Identifying and understanding holes in rational functions is essential for various reasons:
-
Accurate Graphing: Holes create gaps in the graph; neglecting them leads to an inaccurate representation.
-
Analysis of Function Behavior: Holes are crucial for analyzing the function's limits, continuity, and overall behavior near the discontinuity.
-
Applications in Calculus: In calculus, the concept of removable discontinuities is important for understanding derivatives and integrals.
-
Real-world Applications: Rational functions model numerous real-world phenomena, and understanding holes helps interpret the models accurately. For example, in physics, a hole might represent a point of instability or a sudden change in a system.
Conclusion
Finding holes in rational functions is a crucial skill in algebra and calculus. By mastering the techniques outlined in this guide, you'll gain a deeper understanding of rational functions and their behavior. Remember to factor completely, carefully identify common factors, and precisely determine the coordinates of the hole. With practice, identifying and graphing these removable discontinuities will become second nature, enabling you to confidently analyze and visualize rational functions with all their nuances. Remember that consistent practice with various examples is key to developing a firm grasp of this concept. So, grab your pencils and start factoring!
Latest Posts
Latest Posts
-
Where Is The 3 In Riddle Transfer
Jul 03, 2025
-
How Much Does A Water Bottle Weight
Jul 03, 2025
-
How Many Inches Is Half A Yard
Jul 03, 2025
-
How Old Are You If Your Born In 1996
Jul 03, 2025
-
How Many Water Bottles In 64 Ounces
Jul 03, 2025
Related Post
Thank you for visiting our website which covers about How To Find A Hole In A Rational Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.