How To Find Coordination Number Of Unit Cell
Kalali
Apr 03, 2025 · 7 min read
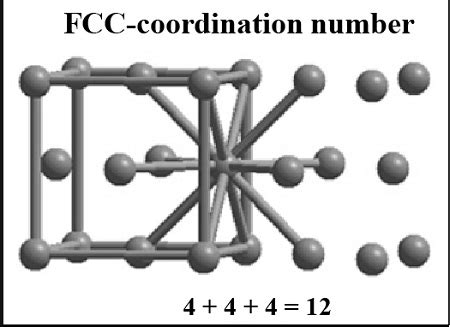
Table of Contents
How to Find the Coordination Number of a Unit Cell: A Comprehensive Guide
Determining the coordination number of atoms within a unit cell is crucial for understanding the structure and properties of crystalline materials. The coordination number represents the number of nearest neighbors surrounding a particular atom in the crystal lattice. This seemingly simple concept underpins many aspects of materials science, influencing properties like density, melting point, and electrical conductivity. This comprehensive guide will explore various methods to determine the coordination number, catering to different levels of understanding, from basic principles to more advanced techniques.
Understanding the Fundamentals
Before delving into the methods, let's establish a firm grasp of fundamental concepts.
What is a Unit Cell?
A unit cell is the smallest repeating unit of a crystal lattice. Think of it as the building block that, when repeated in three dimensions, constructs the entire crystal structure. Different crystal systems (cubic, tetragonal, orthorhombic, etc.) have distinct unit cell geometries defined by their lattice parameters (a, b, c) and interaxial angles (α, β, γ).
What is Coordination Number?
The coordination number (CN) describes the number of atoms directly surrounding a central atom in a crystal structure. These nearest neighbors are typically those at the shortest interatomic distance. The CN is a vital parameter because it influences many material properties. For example, a higher coordination number often implies stronger bonding and a higher melting point.
Types of Crystal Structures and Common Examples
Different crystal structures exhibit varying coordination numbers. Understanding these structures is key to calculating CN. Here are a few common examples:
- Simple Cubic (SC): Atoms are located only at the corners of the cube. The CN is 6.
- Body-Centered Cubic (BCC): Atoms are located at the corners and the center of the cube. The CN is 8.
- Face-Centered Cubic (FCC): Atoms are located at the corners and the centers of each face of the cube. The CN is 12.
- Hexagonal Close-Packed (HCP): Atoms are arranged in a hexagonal pattern. The CN is 12.
These are just the most common structures. Many other complex crystal structures exist, often involving multiple types of atoms and more intricate arrangements.
Methods for Determining Coordination Number
Several methods can be used to determine the coordination number, depending on the complexity of the crystal structure and the available information.
1. Visual Inspection and Simple Counting (For Simple Structures)
For simple structures like SC, BCC, and FCC, a visual inspection of the unit cell can often suffice.
Steps:
- Identify the central atom: Choose an atom within the unit cell.
- Count the nearest neighbors: Count the number of atoms directly touching the central atom. This number represents the coordination number.
Example (BCC):
In a BCC structure, a central atom is surrounded by eight corner atoms. Therefore, the coordination number is 8. Note that atoms on adjacent unit cells are considered nearest neighbors in this context.
Limitations: This method is only suitable for simple structures. For complex structures with multiple atom types or intricate arrangements, this approach becomes impractical and prone to errors.
2. Using the Unit Cell Geometry and Atom Positions (For More Complex Structures)
For more complex structures, a geometrical approach becomes necessary. This involves considering the unit cell dimensions and the precise atomic positions.
Steps:
- Determine the unit cell parameters: Obtain the lattice parameters (a, b, c) and interaxial angles (α, β, γ) of the unit cell.
- Identify atomic positions: Determine the fractional coordinates (x, y, z) of all atoms within the unit cell. These coordinates express the atom's position as a fraction of the unit cell dimensions.
- Calculate distances: Using the distance formula, calculate the distances between the central atom and all other atoms in the unit cell.
- Identify nearest neighbors: Identify the atoms with the shortest distances to the central atom. These are the nearest neighbors.
- Count the nearest neighbors: The number of nearest neighbors represents the coordination number.
Example (FCC):
In an FCC unit cell, an atom at a corner has 12 nearest neighbors: 4 atoms in the same plane, 4 in the plane above, and 4 in the plane below. This geometric approach helps clarify this relatively intuitive result.
Limitations: This method requires precise knowledge of the unit cell parameters and atomic positions, which might not always be readily available for complex or less-studied materials.
3. Utilizing Crystallographic Software and Databases
For complex crystal structures, crystallographic software packages provide powerful tools for visualizing and analyzing structures. These packages can automate the process of determining coordination numbers, overcoming limitations faced by manual methods.
Features of such software:
- 3D visualization: Allows for a detailed visualization of the crystal structure, making it easier to identify nearest neighbors.
- Automated coordination number calculation: Software can automatically calculate coordination numbers based on specified distance criteria.
- Data analysis: Enables analysis of various structural features, including bond lengths, bond angles, and coordination polyhedra.
Example: Materials Studio, VESTA, and Avogadro are popular examples of such software. These tools frequently contain databases of known crystal structures.
Limitations: Requires access to and proficiency in using the chosen software. While mostly automated, careful consideration of the parameters used (e.g., distance cutoff for identifying nearest neighbors) is still needed.
4. Experimental Techniques (X-ray Diffraction and Neutron Diffraction)
Experimental techniques such as X-ray diffraction and neutron diffraction can be used to determine the crystal structure, which can then be used to calculate the coordination number.
How these techniques help:
- X-ray Diffraction: Provides data on the arrangement of atoms in a crystal lattice. Analysis of diffraction patterns allows for the determination of the unit cell parameters and atomic positions.
- Neutron Diffraction: Similar to X-ray diffraction, but provides better information about the positions of light atoms (e.g., hydrogen) due to their higher scattering cross-section for neutrons.
Limitations: These are advanced techniques that require specialized equipment and expertise. Data analysis can be complex and time-consuming.
Factors Influencing Coordination Number
Several factors influence the coordination number:
- Atomic size: Larger atoms tend to have higher coordination numbers because they can accommodate more nearest neighbors.
- Ionic radii: In ionic compounds, the ratio of cation and anion radii influences the coordination number.
- Bonding type: The nature of the chemical bonds (ionic, covalent, metallic) affects the coordination number. For example, covalent bonds often result in lower coordination numbers compared to metallic bonds.
- Packing efficiency: The way atoms are packed in a crystal lattice influences the coordination number. Close-packed structures (like FCC and HCP) have higher coordination numbers.
Applications and Significance of Coordination Number
Understanding the coordination number is paramount in numerous applications:
- Material design: Coordination number plays a vital role in designing materials with specific properties. For example, tailoring the coordination number can lead to materials with enhanced strength, conductivity, or catalytic activity.
- Catalysis: The coordination environment of active sites in catalysts is crucial for catalytic activity. Understanding coordination numbers helps optimize catalyst design.
- Geochemistry: Coordination numbers are essential in understanding the structure and behavior of minerals and other geological materials.
- Solid-state physics: Coordination numbers influence the electronic and magnetic properties of materials.
Conclusion
Determining the coordination number of atoms in a unit cell is crucial for understanding the structure and properties of crystalline materials. This guide has presented different methods—from simple visual inspection for basic structures to sophisticated software and experimental techniques for complex ones. Choosing the appropriate method depends on the complexity of the structure and the available resources. Regardless of the method, understanding the fundamental principles behind coordination numbers and their implications is essential for researchers and students alike in fields ranging from materials science and engineering to geology and chemistry. The continued development and refinement of both theoretical and experimental techniques will further enhance our ability to accurately determine and utilize coordination numbers in a wide range of scientific applications.
Latest Posts
Latest Posts
-
22 Is What Percent Of 40
Apr 04, 2025
-
Is Length An Intensive Or Extensive Property
Apr 04, 2025
-
14 Of 25 Is What Percent
Apr 04, 2025
-
Which Of The Following Are Renewable Resources
Apr 04, 2025
-
Cuanto Es 5 Pies En Pulgadas
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about How To Find Coordination Number Of Unit Cell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
