How To Find Friction Without Coefficient
Kalali
Mar 31, 2025 · 7 min read
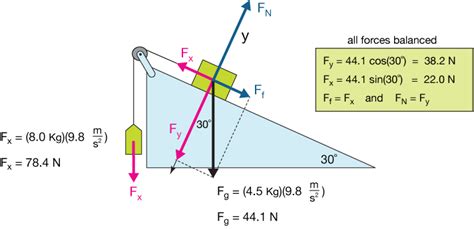
Table of Contents
How to Find Friction Without the Coefficient of Friction
Determining frictional forces without explicitly knowing the coefficient of friction might seem impossible at first. After all, the standard equation, F<sub>friction</sub> = μN, where μ is the coefficient of friction and N is the normal force, is deeply ingrained in our understanding of physics. However, several scenarios allow us to determine frictional forces indirectly, leveraging other physical principles and employing clever experimental setups. This article delves into various methods and situations where calculating friction is feasible even without direct knowledge of the coefficient of friction.
Understanding Friction: A Quick Recap
Before diving into the methods, let's briefly revisit the fundamentals of friction. Friction is a force that opposes motion between two surfaces in contact. It's broadly categorized into two types:
-
Static Friction (F<sub>s</sub>): This force prevents an object from starting to move when a force is applied. The maximum static friction force (F<sub>s,max</sub>) is proportional to the normal force (N), with the proportionality constant being the coefficient of static friction (μ<sub>s</sub>).
-
Kinetic Friction (F<sub>k</sub>): This force opposes the motion of an object already in motion. The kinetic friction force (F<sub>k</sub>) is also proportional to the normal force (N), with the proportionality constant being the coefficient of kinetic friction (μ<sub>k</sub>).
The standard equations, as mentioned before, are:
- F<sub>s,max</sub> = μ<sub>s</sub>N
- F<sub>k</sub> = μ<sub>k</sub>N
However, these equations are only useful when μ<sub>s</sub> and μ<sub>k</sub> are known. Let's explore situations where we can circumvent the need for these coefficients.
Methods to Determine Friction Without the Coefficient
Several scenarios allow us to determine friction without directly utilizing the coefficient of friction. These methods often rely on employing other physical principles like Newton's Laws of Motion, energy conservation, or work-energy theorem.
1. Using Newton's Laws of Motion and Equilibrium
If an object is at rest or moving at a constant velocity on a surface, it's in a state of equilibrium. This means the net force acting on it is zero. We can use this principle to determine the frictional force.
Scenario: Imagine a block resting on an inclined plane. The block is at rest.
Analysis: We can resolve the forces acting on the block into components parallel and perpendicular to the plane. The forces acting are gravity (mg), the normal force (N) perpendicular to the plane, and the static friction force (F<sub>s</sub>) parallel to the plane, opposing the component of gravity parallel to the plane (mg sin θ). Since the block is at rest, the net force is zero:
- ΣF<sub>parallel</sub> = 0 => F<sub>s</sub> - mg sin θ = 0
- ΣF<sub>perpendicular</sub> = 0 => N - mg cos θ = 0
From these equations, we can directly calculate the static friction force (F<sub>s</sub>) without knowing the coefficient of static friction: F<sub>s</sub> = mg sin θ. The normal force is calculated as N = mg cos θ.
This method works equally well for kinetic friction if the block is moving at a constant velocity down the incline. In that case, the equation becomes: F<sub>k</sub> = mg sin θ.
2. Energy Conservation and Work-Energy Theorem
In situations involving motion, the work-energy theorem proves invaluable. This theorem states that the net work done on an object is equal to its change in kinetic energy. Friction dissipates energy as heat, allowing us to relate the work done by friction to the change in kinetic energy.
Scenario: A block slides down a rough inclined plane, starting from rest.
Analysis: As the block slides down, gravity does positive work, while friction does negative work. The work-energy theorem provides:
- W<sub>gravity</sub> + W<sub>friction</sub> = ΔKE
where:
- W<sub>gravity</sub> = mg h (h is the vertical height the block descends)
- W<sub>friction</sub> = -F<sub>k</sub>d (d is the distance the block slides, and the negative sign indicates energy loss due to friction)
- ΔKE = (1/2)mv<sup>2</sup> (v is the final velocity of the block)
By measuring the initial height (h), the final velocity (v), and the distance traveled (d), we can determine the kinetic friction force (F<sub>k</sub>):
- F<sub>k</sub> = (mgh - (1/2)mv<sup>2</sup>) / d
This calculation does not require the coefficient of kinetic friction.
3. Using a Pulley System and Known Masses
This method cleverly uses a system of pulleys and known masses to indirectly determine the frictional force.
Scenario: A block is placed on a horizontal surface connected to a hanging mass via a string passing over a pulley.
Analysis: If the hanging mass is carefully adjusted so that the block moves at a constant velocity, then the tension in the string (T) equals the kinetic friction force (F<sub>k</sub>). The tension is directly related to the weight of the hanging mass (m<sub>hanging</sub>g). Thus, F<sub>k</sub> = m<sub>hanging</sub>g. We don't need to know the coefficient of kinetic friction.
4. Experimental Determination Through Force Measurements
Direct measurement of the frictional force can be achieved using a force sensor.
Scenario: Attach a force sensor to a block resting on a surface.
Analysis: Gradually increase the applied force until the block starts to move. The maximum force measured just before motion is the maximum static friction force. Once the block is moving, the force sensor will register the kinetic friction force if the block is pulled at a constant velocity. This method bypasses the need to know the coefficient of friction. The normal force can be independently determined using a scale.
5. Analyzing Motion with Sensors and Data Logging
Advanced experimental setups can use motion sensors and data loggers to record the block's position and velocity as a function of time.
Analysis: By analyzing the acceleration of the block, we can use Newton's second law (F = ma) to determine the net force acting on the block. Knowing the applied force and the other forces acting, the frictional force can be calculated without explicit knowledge of the coefficient. This method often requires sophisticated data analysis techniques.
Practical Considerations and Limitations
While the methods described above offer viable ways to find friction without relying on the coefficient of friction, some practical considerations and limitations need to be kept in mind:
-
Measurement Accuracy: The accuracy of the results heavily depends on the accuracy of measurements like mass, height, velocity, and distance. Errors in these measurements will propagate into the calculated frictional force.
-
Idealized Conditions: Many of the methods assume idealized conditions, such as neglecting air resistance or assuming perfectly smooth surfaces. In reality, these factors can influence the results.
-
Constant Velocity Assumption: Several methods assume constant velocity. Maintaining constant velocity during experiments can be challenging.
-
Surface Irregularities: The nature of the surfaces in contact significantly affects friction. Micro-level irregularities make it challenging to obtain highly precise results.
-
Temperature Effects: Friction can be temperature-dependent, introducing further complexity.
Conclusion
Determining friction without explicitly knowing the coefficient of friction is achievable through various methods. These methods exploit principles of equilibrium, energy conservation, or direct force measurements. However, it’s crucial to acknowledge the practical considerations and limitations involved in these approaches. The choice of method depends heavily on the specific experimental setup and the level of accuracy required. Careful experimental design, precise measurements, and awareness of potential error sources are vital for obtaining reliable results. Remember to always account for possible systematic and random errors to better understand the uncertainty of your results. By understanding these principles and carefully executing the experiments, one can confidently calculate frictional forces even without explicit knowledge of the coefficient of friction.
Latest Posts
Latest Posts
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
-
How Many Dimes In A 5 Roll
Jul 18, 2025
-
How Do You Say Basil In Spanish
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about How To Find Friction Without Coefficient . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.