How To Find Height Of A Triangular Prism
Kalali
Mar 11, 2025 · 6 min read
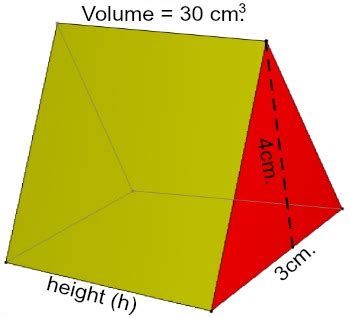
Table of Contents
How to Find the Height of a Triangular Prism: A Comprehensive Guide
Finding the height of a triangular prism might seem straightforward, but the approach varies depending on the information provided. This comprehensive guide will walk you through various scenarios and methods to accurately determine the height of a triangular prism, equipping you with the knowledge to tackle any problem you encounter. We'll explore different approaches, offering step-by-step instructions and clarifying common misconceptions.
Understanding Triangular Prisms and Their Dimensions
A triangular prism is a three-dimensional geometric shape with two parallel triangular bases and three rectangular lateral faces connecting the bases. It's crucial to understand the different dimensions involved:
- Height (h): This is the perpendicular distance between the two triangular bases. It's the measurement we're primarily focused on calculating.
- Base (b): This refers to the length of one side of the triangular base. Note that a triangular prism has three base lengths, and you might need to know all of them depending on the method used.
- Base Height (hb): This is the perpendicular height of one of the triangular bases (the height within the triangle). This is different from the prism's overall height.
- Length (l): This is the length of one of the rectangular lateral faces. There are three such lengths.
- Area of the Base (Ab): This is the area of one of the triangular bases. Calculating this often requires knowing the base and base height of the triangle (using the formula 0.5 * base * base height).
- Volume (V): The volume of the triangular prism, which can be helpful in calculating the height if known.
Methods to Determine the Height of a Triangular Prism
The method you use to find the height depends heavily on the information you already have. Here are the common scenarios and their solutions:
Method 1: Using the Volume and Base Area
This is arguably the most straightforward method if you know the volume and the area of the triangular base. The formula for the volume of a triangular prism is:
V = Ab * h
Where:
- V = Volume
- Ab = Area of the triangular base
- h = Height of the prism
To find the height (h), simply rearrange the formula:
h = V / Ab
Example: A triangular prism has a volume of 75 cubic centimeters and a triangular base area of 15 square centimeters. What is its height?
h = 75 cm³ / 15 cm² = 5 cm
Therefore, the height of the triangular prism is 5 centimeters.
Method 2: Using the Volume, Base Length, and Base Height
If you know the volume, the length of one side of the triangular base, and the base height, you can use the following approach:
-
Calculate the Area of the Base (Ab): Use the formula for the area of a triangle: Ab = 0.5 * base * base height
-
Calculate the Height (h): Use the volume formula from Method 1: h = V / Ab
Example: A triangular prism has a volume of 120 cubic meters, a base length of 10 meters, and a base height of 6 meters.
-
Calculate Ab: Ab = 0.5 * 10 m * 6 m = 30 m²
-
Calculate h: h = 120 m³ / 30 m² = 4 m
The height of the prism is 4 meters.
Method 3: Using Pythagorean Theorem (Right-Angled Triangular Prism)
If the triangular base is a right-angled triangle and you know the lengths of the two shorter sides of the base (legs 'a' and 'b') and the length of a slant height ('s') from the apex of the triangle to a point on the base (where the height meets the base), you can use the Pythagorean theorem. This method is specifically useful for right-angled triangular prisms.
-
Identify the Right Triangle: Find the right-angled triangle formed by the height (h), the base (b), and the slant height (s).
-
Apply Pythagorean Theorem: The Pythagorean theorem states: a² + b² = c². In this case, it will be h² + (base)² = s².
-
Solve for h: Rearrange the equation to solve for the height (h). h = √(s² - base²)
Example: A right-angled triangular prism has a base of 8 cm and a slant height from the apex of the triangle to the base of 10 cm.
-
Identify the Right Triangle: We have a right-angled triangle with hypotenuse 's' (10 cm) and one leg 'base' (8 cm).
-
Apply Pythagorean Theorem: h² + 8² = 10²
-
Solve for h: h² = 100 - 64 = 36. Therefore, h = √36 = 6 cm.
The height of the prism is 6 cm.
Method 4: Using Trigonometry (Non-Right-Angled Triangular Prism)
If you have a triangular prism with a non-right-angled triangular base, you may need to use trigonometry. You will need to know at least one angle and one side length of the base triangle, along with other dimensions of the prism.
This approach involves using trigonometric functions such as sine, cosine, and tangent depending on the information given. More specifically, if you know the slant height (from the apex of one triangular base to its opposite base), the angle between the base and the slant height, and you need to find the height (h), you can use the cosine function.
Example: Suppose you have the slant height (s) and the angle (θ) between the slant height and the base of a triangular prism. You can find the height (h) using the cosine function:
h = s * cos(θ)
Example: A triangular prism has a slant height of 12 cm and the angle between the slant height and the base is 30°.
h = 12 cm * cos(30°) ≈ 10.39 cm
Important Note: The specific trigonometric functions used will depend on the available information. You might need to use sine or tangent depending on the given angles and sides.
Method 5: Using Cross-Sections and Similar Triangles (Advanced Scenario)
In complex scenarios, you might need to utilize cross-sections and the properties of similar triangles. This involves creating a cross-sectional view of the prism and using proportional relationships to find the height. This is a more advanced technique and requires a strong understanding of geometry.
Troubleshooting and Common Mistakes
-
Confusing Height and Base Height: The most common mistake is confusing the height of the prism with the height of the triangular base. Remember, the prism's height is the perpendicular distance between the two bases.
-
Incorrectly Calculating Base Area: Make sure you're using the correct formula for the area of a triangle, accounting for the appropriate base and height.
-
Units: Ensure all measurements are in the same units before performing calculations. Mixing units (e.g., centimeters and meters) will lead to an incorrect answer.
-
Approximations: If using trigonometry or the Pythagorean theorem, be mindful of rounding errors. Use sufficient decimal places during calculations to maintain accuracy.
Conclusion: Mastering Triangular Prism Height Calculation
Calculating the height of a triangular prism is a fundamental skill in geometry. This guide has explored multiple methods, catering to different scenarios and information availability. By understanding the underlying principles and practicing the different approaches, you'll confidently tackle any problem involving triangular prism height calculations. Remember to carefully review the given information, choose the appropriate method, and pay close attention to units and potential sources of error to ensure accurate results.
Latest Posts
Latest Posts
-
If Your 35 What Year Was You Born
Jul 12, 2025
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
-
30 X 30 Is How Many Square Feet
Jul 12, 2025
-
How Much Does A Half Oz Weigh
Jul 12, 2025
-
Calories In An Omelette With 3 Eggs
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about How To Find Height Of A Triangular Prism . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.