How To Find Length Of Chord
Kalali
Apr 01, 2025 · 5 min read
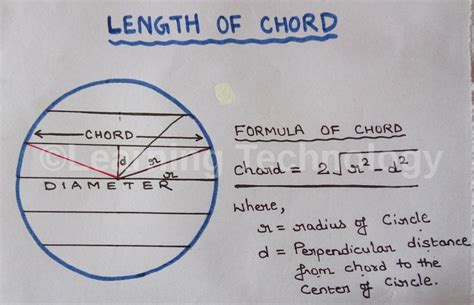
Table of Contents
How to Find the Length of a Chord: A Comprehensive Guide
Finding the length of a chord is a fundamental concept in geometry with applications spanning various fields, from architecture and engineering to computer graphics and game development. Understanding how to calculate chord length involves leveraging different geometric properties and formulas, depending on the information available. This comprehensive guide explores various methods, providing step-by-step instructions and illustrative examples to solidify your understanding.
Understanding Chords and Related Concepts
Before diving into the calculation methods, let's clarify some key definitions:
- Circle: A round plane figure whose boundary (the circumference) consists of points equidistant from a fixed point (the center).
- Chord: A straight line segment whose endpoints both lie on the circumference of a circle. A diameter is a special type of chord that passes through the center of the circle.
- Radius: The distance from the center of a circle to any point on its circumference.
- Diameter: A chord that passes through the center of the circle. It's twice the length of the radius.
- Central Angle: The angle subtended at the center of the circle by the chord.
- Inscribed Angle: The angle subtended by the chord at any point on the circumference.
Methods for Finding Chord Length
The method used to determine the length of a chord depends on the available information. Here are the most common scenarios and their corresponding solutions:
Method 1: Using the Radius and Central Angle
This is arguably the most straightforward method. If you know the radius (r) of the circle and the central angle (θ) subtended by the chord, you can use the following formula:
Chord Length = 2 * r * sin(θ/2)
Where:
- r = radius of the circle
- θ = central angle in degrees or radians (ensure consistency in units).
Example:
Let's say a circle has a radius of 5 cm, and the central angle subtended by a chord is 60°. To find the chord length:
- Convert the central angle to radians if necessary (60° = π/3 radians).
- Apply the formula: Chord Length = 2 * 5 cm * sin(π/3 / 2) = 2 * 5 cm * sin(π/6) = 2 * 5 cm * 0.5 = 5 cm.
Method 2: Using the Radius and the Distance from the Chord to the Center
This method is useful when you know the radius (r) and the perpendicular distance (d) from the center of the circle to the chord. This distance bisects both the chord and the central angle. We can use the Pythagorean theorem:
Chord Length = 2 * √(r² - d²)
Example:
Consider a circle with a radius of 8 cm. The perpendicular distance from the center of the circle to the chord is 3 cm. To find the chord length:
- Apply the formula: Chord Length = 2 * √(8² - 3²) = 2 * √(64 - 9) = 2 * √55 ≈ 14.83 cm.
Method 3: Using the Inscribed Angle and the Diameter
If you know the inscribed angle (α) subtended by the chord and the diameter (D) of the circle, you can use the following method:
This approach leverages the relationship between the inscribed angle and the central angle. The central angle is always double the inscribed angle (θ = 2α). Then you can utilize Method 1, substituting the diameter (D) for 2r:
- Find the central angle: θ = 2α
- Apply the formula: Chord Length = D * sin(θ/2) = D * sin(α)
Example:
Assume the diameter of the circle is 10 cm, and the inscribed angle is 30°. Therefore:
- Central angle (θ) = 2 * 30° = 60°
- Chord Length = 10 cm * sin(30°) = 10 cm * 0.5 = 5 cm.
Method 4: Using Coordinate Geometry
If the endpoints of the chord are known in a Cartesian coordinate system (x₁, y₁) and (x₂, y₂), you can use the distance formula:
Chord Length = √[(x₂ - x₁)² + (y₂ - y₁)²]
Example:
Suppose the endpoints of a chord are (2, 3) and (8, 7).
- Apply the formula: Chord Length = √[(8 - 2)² + (7 - 3)²] = √(6² + 4²) = √(36 + 16) = √52 ≈ 7.21 units.
Advanced Scenarios and Considerations
While the methods above cover common scenarios, more complex situations might require additional steps or different approaches. For instance:
- Finding the chord length within a segment of a circle: This often involves utilizing trigonometric functions and considering the relationships between arcs, angles, and chords within that specific segment.
- Chords intersecting within a circle: Understanding the properties of intersecting chords (the product of the segments of one chord equals the product of the segments of the other) can be crucial in solving such problems.
- Three-dimensional considerations: Extending these concepts to three dimensions (e.g., finding the length of a chord on the surface of a sphere) involves utilizing spherical trigonometry and more advanced mathematical techniques.
Practical Applications
Understanding chord length calculations has practical implications across various disciplines:
- Engineering and Architecture: Calculating distances across circular structures, determining the dimensions of arches, and designing curved components.
- Computer Graphics and Game Development: Creating realistic circular objects, simulating movement along circular paths, and developing collision detection algorithms.
- Surveying and Mapping: Measuring distances and determining locations using circular referencing systems.
- Astronomy: Analyzing celestial bodies and their movements, and calculating distances within orbital paths.
Conclusion
Mastering the ability to calculate chord length is a valuable skill for anyone working with circles and related geometric figures. By understanding the different methods outlined in this guide and their corresponding formulas, you can effectively solve a wide range of problems, regardless of the available information. Remember to choose the appropriate method based on the given parameters and always double-check your calculations for accuracy. Practice is key to solidifying your understanding and improving your proficiency in applying these principles. The more you work with these methods, the easier it will become to identify the most efficient approach for each specific problem.
Latest Posts
Latest Posts
-
How Many Times Does 3 Go Into 30
Jul 13, 2025
-
In What Episode Of Bleach Does Ichigo Ask Orihime Out
Jul 13, 2025
-
How Much Is 4 Oz Chocolate Chips
Jul 13, 2025
-
How Many Times Does 9 Go Into 70
Jul 13, 2025
-
4 Pics 1 Word Cheat 8 Letters
Jul 13, 2025
Related Post
Thank you for visiting our website which covers about How To Find Length Of Chord . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.