How To Find The Height Of A Triangle Without Area
Kalali
Mar 10, 2025 · 5 min read
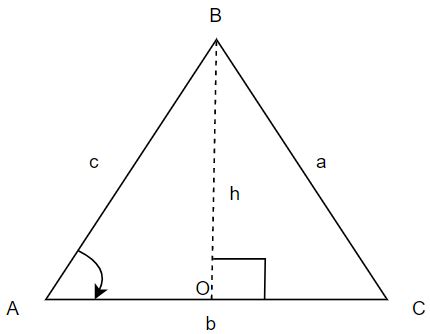
Table of Contents
How to Find the Height of a Triangle Without the Area
Determining the height of a triangle is a fundamental concept in geometry, crucial for calculating its area and solving various geometric problems. While the most common formula for a triangle's area utilizes base and height, many scenarios present situations where the area is unknown. This comprehensive guide explores several methods to find the height of a triangle without relying on its area. We'll delve into different triangle types, utilizing various geometric principles and trigonometric functions to achieve our goal. Let's embark on this geometrical journey!
Understanding Triangle Heights
Before we dive into the methods, let's clarify what we mean by "height" in a triangle. The height, also known as the altitude, is the perpendicular distance from a vertex (corner) to the opposite side (base). Crucially, a triangle has three heights, one for each base and corresponding vertex. These heights intersect at a single point called the orthocenter.
Types of Triangles and Their Properties
The approach to finding the height depends heavily on the type of triangle:
- Right-angled Triangles: These triangles possess a 90-degree angle. Finding the height is often straightforward using Pythagorean theorem or trigonometric functions.
- Equilateral Triangles: All sides are equal in length. The height can be calculated using the properties of 30-60-90 triangles.
- Isosceles Triangles: Two sides are equal in length. The height to the unequal side bisects it.
- Scalene Triangles: All sides are of different lengths. This scenario often requires using trigonometric functions or Heron's formula (indirectly, to find the area, which we are avoiding here).
Methods to Find Triangle Height Without Area
Now, let's explore different techniques to calculate the height of a triangle without using its area:
1. Using Pythagorean Theorem (Right-Angled Triangles)
This is the simplest method, applicable only to right-angled triangles. The Pythagorean theorem states that in a right-angled triangle with hypotenuse 'c' and sides 'a' and 'b', a² + b² = c².
Scenario: Suppose you have a right-angled triangle with hypotenuse of length 10 and one leg of length 6. To find the height (which is the other leg in this case), simply apply the theorem:
- a² + b² = c²
- 6² + b² = 10²
- 36 + b² = 100
- b² = 64
- b = 8 (The height)
2. Trigonometry: Sine, Cosine, and Tangent
Trigonometric functions offer a powerful tool for determining the height of any triangle, provided you know at least one side and one angle.
- Using Sine: If you know one side (a) and the angle opposite to that side (A), you can calculate the height (h) using the formula: h = a * sin(B) (where B is the angle between a and h). Note that A and B are angles of the triangle, and this assumes that the chosen base is the side opposite to angle A.
- Using Cosine: If you know two sides (a and b) and the angle (C) between them, you can calculate the height (h) to side 'a' using the formula: h = b * sin(C).
- Using Tangent: If you know the base (b) and an angle (A) adjacent to it, the height (h) can be determined using: h = b * tan(A). This applies if the angle A is at the base b.
Example: Consider a triangle with side a = 8, angle A = 30°, and angle B = 100°. To find the height to side a (h):
h = a * sin(B) = 8 * sin(100°) ≈ 7.88
3. Properties of Equilateral Triangles
An equilateral triangle has all sides equal in length. The height divides it into two congruent 30-60-90 triangles. The height acts as the longer leg in these smaller triangles.
Let 's' be the side length of the equilateral triangle. The height (h) can be found using the Pythagorean theorem:
- h² + (s/2)² = s²
- h² = s² - (s²/4) = (3s²/4)
- h = s√3 / 2
4. Properties of Isosceles Triangles
An isosceles triangle has two equal sides. The height drawn to the unequal side bisects it. This creates two congruent right-angled triangles. If you know the lengths of the equal sides (a) and the unequal side (b), you can use the Pythagorean theorem. Let 'h' be the height to the unequal side.
- h² + (b/2)² = a²
- h² = a² - (b²/4)
- h = √(a² - (b²/4))
5. Coordinate Geometry Approach
If you know the coordinates of the three vertices of the triangle (x1, y1), (x2, y2), and (x3, y3), you can use the distance formula and the formula for the slope of a line to find the height.
This method is more complex than others, involving multiple steps and calculations of slopes, equations of lines, and distances.
6. Using the Circumradius and Inradius (Advanced)
For more advanced scenarios, the circumradius (R) and inradius (r) of the triangle can be used in conjunction with other known information. The relationships between the sides, angles, heights, circumradius, and inradius are intricate and involve trigonometric identities. This is a very advanced method that requires a thorough understanding of triangle geometry and trigonometric identities.
Choosing the Right Method
The most appropriate method for finding the height of a triangle without the area depends entirely on the available information:
| Available Information | Best Method |
|---|---|
| Right-angled triangle, two sides | Pythagorean theorem |
| One side, two angles | Trigonometry (Sine, Cosine, or Tangent) |
| Equilateral triangle, side length | Properties of equilateral triangles |
| Isosceles triangle, two sides, unequal side | Pythagorean Theorem applied to half the isosceles triangle |
| Coordinates of vertices | Coordinate Geometry |
| Advanced scenarios with circumradius/inradius | Advanced formulas using circumradius and inradius |
Practical Applications
Determining the height of a triangle without relying on its area finds applications in various fields:
- Engineering: Structural engineers utilize triangle heights for calculating stability and stress distribution in triangular structures.
- Surveying: Determining heights of land features involves triangulations and altitude calculations.
- Computer Graphics: Generating 3D models and rendering realistic images often require precise triangle height calculations.
- Physics: Height calculations are essential in solving problems related to projectile motion and inclined planes.
Conclusion
Finding the height of a triangle without knowing its area requires a nuanced approach. By understanding the properties of different triangle types and employing appropriate geometric principles and trigonometric functions, you can effectively determine the height in various situations. Remember to select the most efficient method based on the provided information. Mastering these techniques equips you with a powerful set of tools for solving complex geometrical problems.
Latest Posts
Latest Posts
-
What Is A 56 Out Of 60
Aug 03, 2025
-
How Long Does Brandy Melville Take To Ship
Aug 03, 2025
-
Which Element Is More Likely To Become A Anion
Aug 03, 2025
-
What Do Parables And Fables Have In Common
Aug 03, 2025
-
Her Tears Like Diamonds On The Floor Lyrics
Aug 03, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Height Of A Triangle Without Area . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.