How To Find The Mean In A Dot Plot
Kalali
Apr 03, 2025 · 6 min read
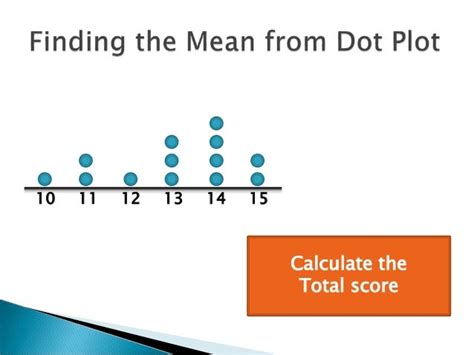
Table of Contents
How to Find the Mean in a Dot Plot: A Comprehensive Guide
Dot plots, also known as dot diagrams, are simple yet powerful statistical tools used to represent data visually. They're particularly useful for showing the distribution of a dataset, highlighting clusters, outliers, and the overall spread of the data. Understanding how to calculate the mean (average) from a dot plot is a fundamental skill in data analysis. This comprehensive guide will walk you through the process, explaining the concepts clearly and providing step-by-step instructions, along with examples to solidify your understanding.
Understanding the Mean and Dot Plots
Before diving into the calculation, let's clarify the key concepts:
What is the Mean? The mean, or average, is a measure of central tendency. It represents the typical or central value of a dataset. It's calculated by summing all the values in the dataset and dividing by the total number of values.
What is a Dot Plot? A dot plot is a simple graph used to display the distribution of a dataset. Each data point is represented by a dot placed above its corresponding value on a number line. The number of dots above each value indicates the frequency of that value in the dataset.
Why Use Dot Plots to Find the Mean? Dot plots offer a visual representation that makes it easier to understand the data before calculating the mean. They allow you to quickly identify the range, frequency of values, and potential outliers which can influence the mean.
Calculating the Mean from a Dot Plot: A Step-by-Step Guide
Let's illustrate the process with an example. Suppose we have a dot plot representing the number of hours students spent studying for an exam:
Example Dot Plot:
*
* *
* * * *
* * * * * *
0 1 2 3 4 5 6 Hours Spent Studying
Step 1: Identify the Values and their Frequencies
From the dot plot, we can see the following values and their frequencies:
- 0 hours: 1 student
- 1 hour: 2 students
- 2 hours: 3 students
- 3 hours: 4 students
- 4 hours: 3 students
- 5 hours: 2 students
- 6 hours: 1 student
Step 2: Calculate the Sum of all Values
To calculate the sum, we multiply each value by its frequency and then add the products together:
(0 hours * 1 student) + (1 hour * 2 students) + (2 hours * 3 students) + (3 hours * 4 students) + (4 hours * 3 students) + (5 hours * 2 students) + (6 hours * 1 student) = 0 + 2 + 6 + 12 + 12 + 10 + 6 = 48 hours
Step 3: Calculate the Total Number of Students
Count the total number of dots in the dot plot. This represents the total number of students:
1 + 2 + 3 + 4 + 3 + 2 + 1 = 16 students
Step 4: Calculate the Mean
Finally, divide the sum of all values (total hours spent studying) by the total number of students:
Mean = Total hours / Total number of students = 48 hours / 16 students = 3 hours
Therefore, the mean number of hours students spent studying for the exam is 3 hours.
Handling Larger Datasets and Outliers
While the above example is relatively small, the process remains the same for larger datasets. The key is to meticulously count the frequencies of each value. For larger datasets, a table might be more helpful to organize the data before calculating the sum.
Outliers and their Influence:
Outliers, which are data points significantly different from the rest of the data, can significantly affect the mean. For instance, if one student studied for 20 hours, the mean would increase considerably. It's important to be aware of outliers and consider their impact on the interpretation of the mean. Sometimes, it's more appropriate to use other measures of central tendency, such as the median (the middle value when the data is ordered), which is less sensitive to outliers.
Practical Applications and Interpretation of the Mean in Dot Plots
The ability to calculate the mean from a dot plot has various applications across different fields:
- Education: Analyzing student performance on tests, assignments, or projects.
- Business: Studying sales figures, customer satisfaction ratings, or production output.
- Science: Analyzing experimental data, measuring biological variables, or studying environmental factors.
- Healthcare: Tracking patient health indicators, analyzing treatment outcomes, or studying disease prevalence.
Interpreting the Mean: The mean provides a single value that summarizes the central tendency of the data. However, it's crucial to consider the context and limitations of the mean. A high mean might indicate high performance or positive outcomes, while a low mean might suggest otherwise. However, the mean alone doesn't tell the whole story. Always consider the overall distribution of the data as shown in the dot plot to gain a more comprehensive understanding. The presence of outliers, the spread of the data, and the shape of the distribution are all important factors to consider alongside the mean.
Beyond the Mean: Exploring Other Statistical Measures from Dot Plots
While the mean is a valuable measure, it’s not always the best representation of the data, especially when outliers are present. Dot plots can help visualize other statistical measures:
-
Median: The middle value when the data is ordered. The median is less affected by outliers than the mean. To find the median from a dot plot, simply order the values and identify the middle one (or the average of the two middle values if there's an even number of data points).
-
Mode: The most frequent value. In a dot plot, this is easily identified as the value with the most dots above it.
-
Range: The difference between the highest and lowest values. This can be directly observed in the dot plot by subtracting the smallest value from the largest value.
Understanding these additional statistical measures, alongside the mean, provides a more complete picture of the data represented in a dot plot.
Advanced Techniques and Considerations
For more complex datasets, software packages like Excel, R, or Python can automate the calculation of the mean and other statistical measures from data represented in a dot plot or other formats. These tools also offer sophisticated visualization options to better understand the data distribution.
Data Cleaning: Before calculating the mean from a dot plot, it’s important to ensure the data is clean and accurate. Errors in data entry can skew the results.
Data Transformation: In some cases, transforming the data (e.g., using logarithmic transformations) might be necessary to improve the interpretability of the mean and the overall analysis.
Conclusion: Mastering the Mean in Dot Plots
The ability to calculate and interpret the mean from a dot plot is a fundamental skill in data analysis. This guide provided a step-by-step approach, demonstrating how to efficiently calculate the mean from a visual representation of the data. Remember to always consider the context of the data, potential outliers, and other statistical measures to gain a complete understanding of the dataset. By mastering these techniques, you can effectively analyze and interpret data, making informed decisions based on a strong foundation in statistical understanding. Remember that while the mean offers a valuable summary, it is just one piece of the puzzle. Combining it with visual representations like dot plots and other statistical measures leads to a more robust and nuanced interpretation of your data.
Latest Posts
Latest Posts
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
-
How Many Dimes In A 5 Roll
Jul 18, 2025
-
How Do You Say Basil In Spanish
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Mean In A Dot Plot . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.