How To Integrate X 2 1 X 2
Kalali
May 20, 2025 · 2 min read
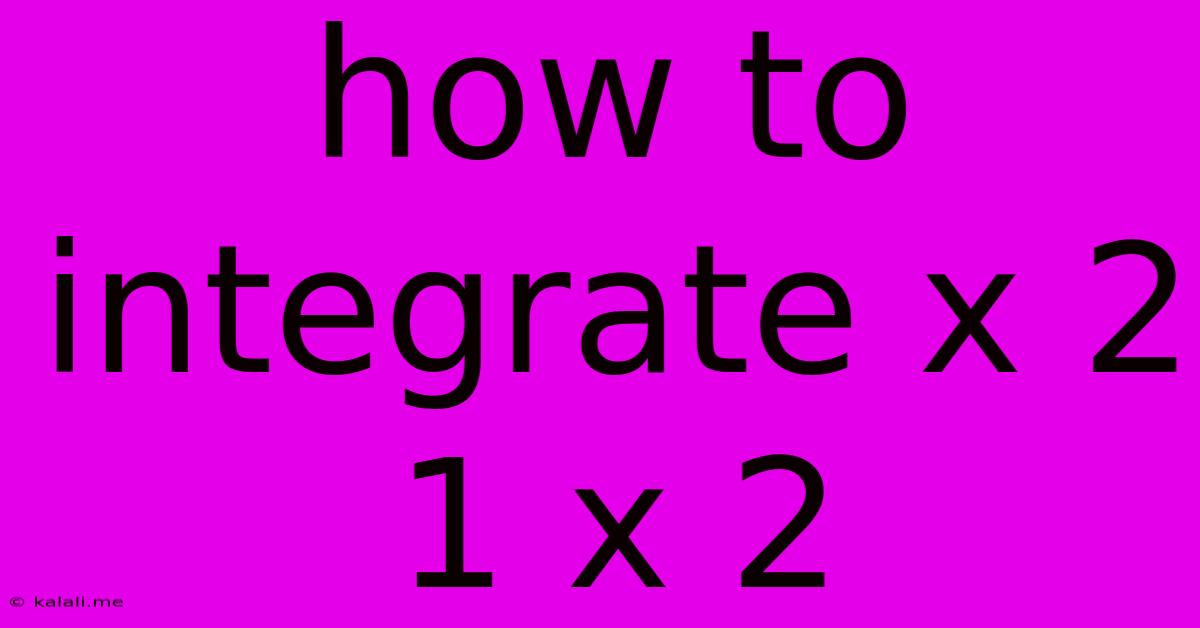
Table of Contents
How to Integrate x²/(1+x²)
This article will guide you through the process of integrating the function x²/(1+x²). This integral is a classic example that combines several integration techniques and provides a great illustration of how to approach complex integration problems. Understanding this process will enhance your calculus skills significantly. We'll explore different methods and demonstrate how to arrive at the solution effectively.
Understanding the Integrand
The integrand, x²/(1+x²), presents a challenge because we can't directly apply a simple power rule. It requires a bit of manipulation to make it integrable. The key here is recognizing that we can rewrite the integrand using polynomial long division or a clever algebraic trick.
Method 1: Polynomial Long Division
The most straightforward approach is to use polynomial long division to simplify the integrand. Dividing x² by (1+x²) gives:
x² / (1+x²) = 1 - 1/(1+x²)
Now, the integral becomes significantly easier:
∫x²/(1+x²) dx = ∫[1 - 1/(1+x²)] dx
This integral can now be solved using basic integration rules:
∫1 dx = x + C₁
and
∫1/(1+x²) dx = arctan(x) + C₂
Therefore, the final solution using this method is:
∫x²/(1+x²) dx = x - arctan(x) + C (where C = C₁ + C₂ is the constant of integration)
Method 2: Algebraic Manipulation
Alternatively, we can manipulate the integrand algebraically. Add and subtract 1 from the numerator:
x²/(1+x²) = (x² + 1 - 1) / (1+x²) = (1+x²)/(1+x²) - 1/(1+x²) = 1 - 1/(1+x²)
This leads us to the same integral as in Method 1, resulting in the identical solution:
∫x²/(1+x²) dx = x - arctan(x) + C
Understanding the Solution
The solution, x - arctan(x) + C, might seem unexpected. However, it's perfectly valid. The arctangent function, arctan(x), represents the inverse tangent function, giving the angle whose tangent is x. The constant of integration, C, accounts for the fact that there are infinitely many antiderivatives, all differing by a constant.
Verifying the Solution (Differentiation)
To verify our solution, we can differentiate it and see if we get back the original integrand:
d/dx [x - arctan(x) + C] = 1 - 1/(1+x²) = (1+x² - 1)/(1+x²) = x²/(1+x²)
The differentiation confirms that our solution is correct.
Conclusion
Integrating x²/(1+x²) successfully involves simplifying the integrand using polynomial long division or algebraic manipulation. This allows us to apply basic integration rules to obtain the final solution, x - arctan(x) + C. Remember to always verify your solutions by differentiating the result. This problem showcases the importance of algebraic manipulation and strategic application of integration techniques in solving seemingly complex integrals. Mastering these techniques will prove invaluable in your further studies of calculus.
Latest Posts
Latest Posts
-
Do Plug Socket Wires Run Up Or Down Uk
May 20, 2025
-
How To Patch A Small Hole In Plaster Ceiling
May 20, 2025
-
How Long Will Fish Live Without A Filter
May 20, 2025
-
Honeywell Thermostat Wiring Diagram 3 Wire
May 20, 2025
-
How To Shut Hot Water Off
May 20, 2025
Related Post
Thank you for visiting our website which covers about How To Integrate X 2 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.