How To Know If An Quadratic Equation Is Linear
Kalali
Apr 05, 2025 · 5 min read
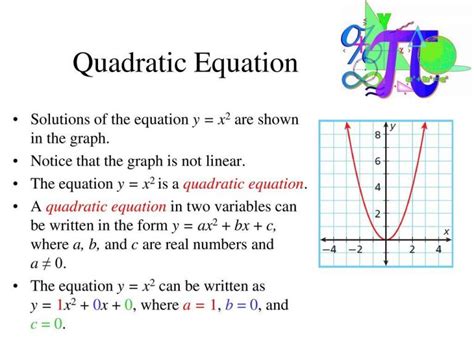
Table of Contents
How to Know if a Quadratic Equation is Linear: A Comprehensive Guide
It's a common misconception that a quadratic equation can somehow morph into a linear equation. The truth is, a quadratic equation is fundamentally different from a linear equation, and they can never be the same. This article will thoroughly explore the distinctions between these two types of equations, clarifying why a quadratic equation can never be linear. We'll delve into the definitions, explore their graphical representations, and examine the algebraic properties that definitively separate them.
Understanding Linear Equations
A linear equation is an algebraic equation of the first degree, meaning the highest power of the variable (usually x) is 1. It can be written in the general form:
y = mx + c
where:
- y and x are variables.
- m represents the slope of the line (rate of change).
- c represents the y-intercept (the point where the line crosses the y-axis).
The graph of a linear equation is always a straight line. This characteristic directly stems from the constant rate of change represented by the slope, 'm'. For every unit increase in x, y changes by a constant amount, 'm'.
Understanding Quadratic Equations
A quadratic equation is an algebraic equation of the second degree, meaning the highest power of the variable (usually x) is 2. It can be written in the general form:
y = ax² + bx + c
where:
- y and x are variables.
- a, b, and c are constants, with 'a' not equal to zero (if a=0, it becomes a linear equation).
The graph of a quadratic equation is always a parabola – a U-shaped curve. This curved shape is a direct consequence of the x² term. The rate of change of y is not constant; it varies depending on the value of x.
Key Differences: Why a Quadratic Equation Can Never Be Linear
The fundamental differences between linear and quadratic equations lie in their:
-
Degree: A linear equation has a degree of 1, while a quadratic equation has a degree of 2. This single difference is the defining characteristic that separates them. The degree dictates the shape of the graph and the behavior of the equation.
-
Graphical Representation: Linear equations always graph as straight lines, while quadratic equations always graph as parabolas. This visual distinction is a clear and immediate way to differentiate between them. No amount of manipulation can transform a parabola into a straight line.
-
Rate of Change: The rate of change (slope) in a linear equation is constant. In a quadratic equation, the rate of change is continuously varying. This means that the slope of the tangent line to the parabola changes at every point along the curve.
-
Number of Roots/Solutions: A linear equation typically has one solution (or root), representing the x-coordinate of the point where the line intersects the x-axis. A quadratic equation can have up to two real solutions (or roots), representing the x-coordinates of the points where the parabola intersects the x-axis. It can also have one repeated root or two complex roots.
-
Algebraic Manipulation: While you can manipulate a quadratic equation algebraically (e.g., completing the square, using the quadratic formula), no algebraic manipulation can reduce the degree of the equation from 2 to 1. You cannot eliminate the x² term without fundamentally changing the nature of the equation.
Common Mistakes and Misconceptions
Some might mistakenly think a quadratic equation becomes linear under certain conditions. Let's address these misconceptions:
-
Setting x = 0: If you substitute x = 0 into a quadratic equation, you obtain a single point on the parabola. This doesn't transform the equation into a linear one; it merely gives you one point on the curve. The equation remains quadratic.
-
Ignoring the x² term: Ignoring the x² term fundamentally alters the equation, turning it into a linear equation. However, this is not a legitimate transformation; it's simply creating a different, unrelated equation.
-
Considering special cases: Certain quadratic equations might seem to resemble lines within a limited domain. For example, a parabola with a very small 'a' value might appear almost flat over a small interval. However, this is just a visual approximation; zooming out will always reveal the parabolic curve. The equation remains intrinsically quadratic.
-
Linear approximations: In calculus, we use linear approximations (tangent lines) to approximate the behavior of a function (such as a quadratic) near a specific point. This linear approximation is a different equation from the original quadratic; it's an approximation useful for specific purposes, not a transformation of the quadratic itself.
Practical Examples and Illustrations
Let's consider some examples to solidify the concept:
Example 1:
y = 2x² + 3x - 1 (Quadratic)
This is a standard quadratic equation. Its graph is a parabola. No amount of algebraic manipulation will change this.
Example 2:
y = x (Linear)
This is a simple linear equation. Its graph is a straight line with a slope of 1 and a y-intercept of 0.
Example 3 (Addressing Misconceptions):
y = 0.01x² + x + 5
While the parabola defined by this equation might appear almost linear over a small range of x values due to the small coefficient of x², it remains fundamentally a quadratic equation. The x² term persists, determining the parabolic nature of the graph.
Conclusion: The Irreducible Nature of Quadratic Equations
In summary, a quadratic equation can never become a linear equation. Their fundamental differences in degree, graphical representation, rate of change, and number of solutions are insurmountable. While algebraic manipulations and approximations might seem to suggest otherwise, these actions don't fundamentally change the nature of the quadratic equation. The presence of the x² term irrefutably defines it as a quadratic, distinct from a linear equation. Understanding this distinction is critical for accurate mathematical modeling and problem-solving. Always remember that a quadratic equation, with its parabolic form, possesses properties entirely different from those of a linear equation and its straight-line graph. The two are fundamentally and inherently distinct.
Latest Posts
Latest Posts
-
How Many Months Is A Hundred Days
Jul 18, 2025
-
Mother And I Or Mother And Me
Jul 18, 2025
-
How Many Oz In One Water Bottle
Jul 18, 2025
-
How Many Dimes In A 5 Roll
Jul 18, 2025
-
How Do You Say Basil In Spanish
Jul 18, 2025
Related Post
Thank you for visiting our website which covers about How To Know If An Quadratic Equation Is Linear . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.