How To Multiply Fractions With Square Roots
Kalali
Mar 31, 2025 · 5 min read
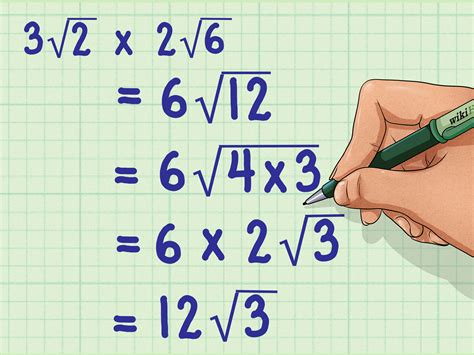
Table of Contents
How to Multiply Fractions with Square Roots: A Comprehensive Guide
Multiplying fractions containing square roots might seem daunting at first, but with a systematic approach, it becomes straightforward. This comprehensive guide breaks down the process step-by-step, covering various scenarios and providing ample examples to solidify your understanding. We'll explore the fundamental rules of fraction multiplication, the properties of square roots, and how to combine these concepts effectively. By the end, you'll be confidently tackling even the most complex problems involving fractions and square roots.
Understanding the Fundamentals: Fractions and Square Roots
Before diving into multiplication, let's refresh our understanding of fractions and square roots.
Fractions: A Quick Recap
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top) and the denominator (bottom). For example, in the fraction ¾, 3 is the numerator and 4 is the denominator.
Key concepts:
- Simplifying fractions: Reducing a fraction to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, ⁶⁄₈ simplifies to ³⁄₄ (dividing both by 2).
- Multiplying fractions: Multiply the numerators together and the denominators together. For example, (²⁄₃) * (⁴⁄₅) = ⁸⁄₁₅.
Square Roots: Unveiling the Basics
The square root of a number (√x) is a value that, when multiplied by itself, equals the original number (x). For example, √9 = 3 because 3 * 3 = 9.
Key properties:
- Product rule for square roots: √(a * b) = √a * √b. This means you can separate the square root of a product into the product of the square roots.
- Quotient rule for square roots: √(a / b) = √a / √b. Similarly, you can separate the square root of a quotient into the quotient of the square roots.
- Simplifying square roots: Finding the largest perfect square that is a factor of the number under the square root and then simplifying. For example, √12 = √(4 * 3) = √4 * √3 = 2√3.
Multiplying Fractions with Square Roots: A Step-by-Step Approach
Now, let's combine these concepts to master the multiplication of fractions containing square roots. The process generally involves three main steps:
- Multiply the numerators: Multiply the numbers in the numerator, remembering to apply the product rule for square roots if needed.
- Multiply the denominators: Multiply the numbers in the denominator, again using the product rule for square roots if applicable.
- Simplify the resulting fraction: Simplify the fraction by canceling common factors in the numerator and denominator, and simplifying any remaining square roots.
Examples: Gradual Progression
Let's work through several examples, starting with simpler cases and progressing to more complex ones.
Example 1: Simple Multiplication
(√2 / 3) * (√8 / 5)
- Multiply numerators: √2 * √8 = √(2 * 8) = √16 = 4
- Multiply denominators: 3 * 5 = 15
- Simplify: The resulting fraction is ⁴⁄₁₅.
Example 2: Incorporating Simplification
(√12 / 4) * (√3 / 6)
- Multiply numerators: √12 * √3 = √(12 * 3) = √36 = 6
- Multiply denominators: 4 * 6 = 24
- Simplify: ⁶⁄₂₄ simplifies to ¹⁄₄.
Example 3: Dealing with Variables
(√(2x) / 5) * (√(8x) / 3)
- Multiply numerators: √(2x) * √(8x) = √(16x²) = 4x (Assuming x is non-negative)
- Multiply denominators: 5 * 3 = 15
- Simplify: The resulting fraction is (4x) / 15.
Example 4: More Complex Scenarios
(3√2 + √6) / 4 * (√3 / 2)
This example involves a binomial expression in the numerator of the first fraction. We need to distribute the second fraction:
- Distribute: [(3√2 * √3) + (√6 * √3)] / (4 * 2)
- Simplify square roots: [3√6 + √18] / 8
- Further simplification: √18 can be simplified to 3√2, so we have [3√6 + 3√2] / 8. This fraction cannot be simplified further.
Example 5: Rationalizing the Denominator
(√5 / √2) * (√3 / 2)
While not strictly part of multiplication, often we need to rationalize the denominator to obtain a more standard form. We'll multiply both the numerator and denominator by √2:
- Multiply: (√5 * √3) / (√2 * 2) = √15 / (2√2)
- Rationalize the denominator: Multiply both numerator and denominator by √2. (√15 * √2) / (2√2 * √2) = √30 / 4
Advanced Techniques and Considerations
Rationalizing the Denominator
As illustrated above, rationalizing the denominator removes square roots from the denominator, resulting in a more simplified and manageable expression. This is especially important when dealing with complex fractions or when preparing for further calculations.
Working with Radicals in the Denominator
When you encounter expressions like 1/(√a + √b), you need to multiply the numerator and denominator by the conjugate (√a - √b) to eliminate the square roots in the denominator. This process uses the difference of squares formula: (a + b)(a - b) = a² - b².
Combining Like Terms
After multiplying fractions with square roots, always simplify the result by combining like terms (terms with the same square root).
Troubleshooting Common Mistakes
- Incorrect application of the product/quotient rules: Ensure that you are correctly applying the product rule (√a * √b = √(a*b)) and quotient rule (√a / √b = √(a/b)) for square roots.
- Forgetting to simplify: Always simplify fractions to their lowest terms and simplify square roots as much as possible.
- Errors in distribution: When dealing with binomial expressions in the numerator, be careful to distribute correctly.
- Not rationalizing the denominator: Remember to rationalize the denominator when necessary to obtain a standard mathematical form.
Conclusion: Mastering the Art of Multiplication
Multiplying fractions containing square roots is a fundamental skill in algebra and beyond. By understanding the basic principles of fractions and square roots, and following the systematic steps outlined in this guide, you can confidently tackle various problems, from simple multiplications to more complex scenarios involving rationalization and simplification. Remember to practice regularly, review the examples, and address any common mistakes. With consistent effort, you'll become proficient in this essential mathematical operation.
Latest Posts
Latest Posts
-
A Limit Involving The Cosine Function
Apr 02, 2025
-
How Much Is 36 Inches In Feet
Apr 02, 2025
-
What Is A 5 Out Of 7
Apr 02, 2025
-
61 5 Inches Is How Many Feet
Apr 02, 2025
-
What Is 4 9 In Inches
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about How To Multiply Fractions With Square Roots . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
