How To Turn An Improper Fraction Into A Proper Fraction
Kalali
Mar 14, 2025 · 5 min read
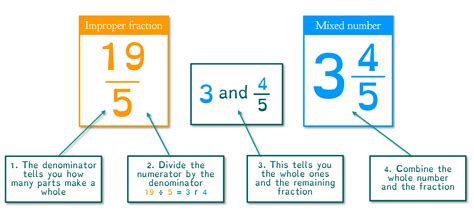
Table of Contents
How to Turn an Improper Fraction into a Proper Fraction: A Comprehensive Guide
Improper fractions, those where the numerator (top number) is greater than or equal to the denominator (bottom number), can seem intimidating. But converting them into mixed numbers (a whole number and a proper fraction) is a fundamental skill in mathematics, crucial for various applications from baking to advanced calculus. This comprehensive guide will demystify the process, offering various methods and clarifying common misconceptions. We'll explore not just the how, but also the why, ensuring you grasp the underlying concepts and can confidently tackle any improper fraction.
Understanding Improper Fractions and Mixed Numbers
Before diving into the conversion process, let's solidify our understanding of the key terms:
-
Improper Fraction: A fraction where the numerator is greater than or equal to the denominator. Examples include 7/4, 5/5, and 11/3.
-
Proper Fraction: A fraction where the numerator is smaller than the denominator. Examples include 1/4, 2/5, and 3/8.
-
Mixed Number: A number consisting of a whole number and a proper fraction. Examples include 1 ¾, 2 ⅓, and 3 ⅛.
The core idea behind converting an improper fraction to a mixed number is to represent the same quantity in a different, more readily interpretable format. An improper fraction represents a value greater than or equal to one, while a mixed number explicitly shows the whole number component and the remaining fractional part.
Method 1: Division – The Fundamental Approach
This method forms the bedrock of converting improper fractions. It's based on the very definition of a fraction: a fraction represents division.
Steps:
-
Divide the numerator by the denominator. Perform the division as you would with any two numbers. For example, let's convert 7/4: 7 ÷ 4 = 1 with a remainder of 3.
-
The quotient becomes the whole number. The result of the division (1 in this case) becomes the whole number part of your mixed number.
-
The remainder becomes the numerator of the proper fraction. The remainder (3 in this case) becomes the numerator of the proper fraction.
-
The denominator remains unchanged. The denominator of the improper fraction (4 in this case) remains the denominator of the proper fraction.
Therefore, 7/4 converts to 1 ¾.
Example 2: Converting 11/3
- 11 ÷ 3 = 3 with a remainder of 2.
- The whole number is 3.
- The remainder is 2.
- The denominator remains 3.
Therefore, 11/3 converts to 3 ⅔.
Example 3: Converting 5/5
- 5 ÷ 5 = 1 with a remainder of 0.
- The whole number is 1.
- The remainder is 0. This means there's no fractional part left.
Therefore, 5/5 converts to 1.
Method 2: Repeated Subtraction – A Visual Approach
This method offers a more visual and intuitive understanding of the conversion process. It's particularly helpful for beginners.
Steps:
-
Subtract the denominator from the numerator repeatedly until the result is less than the denominator. For instance, let's convert 11/3:
11 - 3 = 8 8 - 3 = 5 5 - 3 = 2
-
The number of times you subtracted is the whole number. We subtracted 3 three times, so our whole number is 3.
-
The remaining value is the numerator of the proper fraction. The remaining value after the repeated subtraction is 2.
-
The denominator remains unchanged. The denominator remains 3.
Therefore, 11/3 converts to 3 ⅔. This method visually demonstrates how many "whole" denominators are contained within the numerator.
Method 3: Using Equivalent Fractions – A Less Common but Valuable Method
This method relies on the concept of equivalent fractions. While less direct than the previous methods, it reinforces the understanding of fractional equivalence.
Steps:
-
Find an equivalent fraction with a numerator that's a multiple of the denominator. Let's convert 7/4. We know that 4 x 1 = 4 and 4 x 2 = 8. Since 8 is close to 7, this won't work directly. Instead, let's consider the equivalent fraction approach differently. 7/4 is equivalent to (4/4) + (3/4), which simplifies to 1 + (3/4) = 1 ¾
-
Separate the fraction into a sum of whole numbers and a proper fraction. We can rewrite 7/4 as 4/4 + 3/4.
-
Simplify the whole number part. 4/4 simplifies to 1.
Therefore, 7/4 converts to 1 ¾. This method requires a bit of intuition to identify the appropriate equivalent fraction but helps build conceptual understanding of fraction equivalence and manipulation.
Common Mistakes to Avoid
-
Incorrect division: Ensure accurate division when using the division method. A small error in division can lead to a completely wrong mixed number.
-
Misinterpreting the remainder: The remainder is crucial. Don't overlook it or misinterpret its role in forming the proper fraction.
-
Forgetting the denominator: The denominator of the improper fraction remains the same in the resulting proper fraction. Don't change it.
-
Not simplifying the final answer: Always simplify the proper fraction part of the mixed number if possible. For example, 6/8 should be simplified to 3/4.
Applications of Improper Fraction to Mixed Number Conversion
The ability to convert improper fractions to mixed numbers is vital in numerous real-world situations and mathematical contexts:
-
Cooking and Baking: Recipes often use mixed numbers for ingredient quantities. Converting improper fractions ensures accurate measurements.
-
Construction and Engineering: Precise measurements are crucial, and improper fractions might need conversion for practical application.
-
Data Analysis and Statistics: Representing data using mixed numbers can offer a clearer understanding than using solely improper fractions.
-
Advanced Mathematics: Calculus and other advanced mathematical concepts frequently involve manipulating fractions, and converting between improper fractions and mixed numbers is a necessary step.
Beyond the Basics: Working with Negative Improper Fractions
The same principles apply to negative improper fractions. Simply convert the improper fraction to a mixed number as shown above, and then apply the negative sign to the resulting mixed number. For example:
-11/3 converts to -3 ⅔
Conclusion: Mastering Improper Fraction Conversion
Converting improper fractions to mixed numbers is a foundational skill in mathematics. Understanding the underlying principles, whether through division, repeated subtraction, or equivalent fractions, empowers you to approach these conversions with confidence. Remember to practice regularly, focusing on accuracy and avoiding common errors. Mastering this skill lays a solid foundation for more advanced mathematical concepts and real-world applications. By consistently applying these methods and understanding the underlying logic, you'll transform your approach to fractions, making them less daunting and more manageable.
Latest Posts
Latest Posts
-
Prepare Me A Body And I Will Redeem Man
Jul 10, 2025
-
How Many Inches Is A Meter Stick
Jul 10, 2025
-
Soundtrack To Step Up 2 The Streets
Jul 10, 2025
-
Keebler Club And Cheddar Crackers Expiration Date
Jul 10, 2025
-
In Many States Trailers With A Gvwr Of 1500
Jul 10, 2025
Related Post
Thank you for visiting our website which covers about How To Turn An Improper Fraction Into A Proper Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.