How To Use Rationalizing To Calculating Limits
Kalali
Apr 02, 2025 · 5 min read
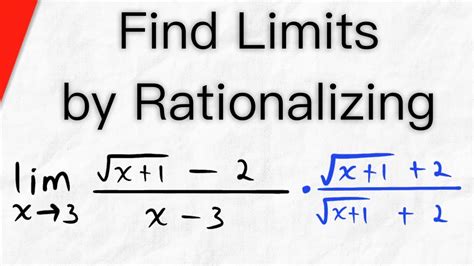
Table of Contents
How to Use Rationalizing to Calculate Limits
Calculating limits can be tricky, but sometimes a clever algebraic manipulation can make seemingly impossible problems straightforward. One such technique is rationalizing, a method particularly useful when dealing with limits involving radicals (square roots, cube roots, etc.) or expressions that result in indeterminate forms like 0/0 or ∞/∞. This comprehensive guide will explore the intricacies of using rationalization to evaluate limits, providing you with a solid understanding and practical examples.
Understanding Indeterminate Forms and the Need for Rationalization
Before diving into the technique, let's refresh our understanding of indeterminate forms. These are expressions that don't provide a clear answer when directly substituting the limit value. The most common indeterminate forms are:
- 0/0: This arises when both the numerator and the denominator approach zero.
- ∞/∞: This occurs when both the numerator and the denominator approach infinity.
These forms don't inherently mean the limit doesn't exist; they simply indicate that further manipulation is needed to determine the limit's true value. Rationalization is a powerful tool for resolving these indeterminate forms, especially when dealing with expressions involving radicals.
The Rationalization Technique: A Step-by-Step Guide
Rationalization involves manipulating an expression by multiplying the numerator and denominator by a strategically chosen conjugate. The conjugate of an expression is created by changing the sign between the terms.
1. Identify the Radical Expression: The first step is to identify the expression containing the radical that's causing the indeterminate form. This will often be in the numerator or denominator, or potentially both.
2. Determine the Conjugate: Next, find the conjugate of the identified radical expression. For example:
- The conjugate of (√x + 2) is (√x - 2).
- The conjugate of (3 - √(x+1)) is (3 + √(x+1)).
- The conjugate of (√x - √y) is (√x + √y).
3. Multiply the Numerator and Denominator by the Conjugate: This is the core of the rationalization process. Remember, multiplying both the numerator and denominator by the same expression is equivalent to multiplying by 1, thus not changing the value of the original expression.
4. Simplify the Expression: After multiplying, use algebraic techniques to simplify the resulting expression. This often involves expanding the numerator and denominator, canceling common terms, and potentially applying difference of squares factorization: (a + b)(a - b) = a² - b². This step is crucial in eliminating the indeterminate form.
5. Substitute the Limit Value: Once the expression is simplified and the indeterminate form is removed, substitute the limit value into the expression to find the limit.
Examples: Illustrating Rationalization in Action
Let's work through several examples to solidify our understanding.
Example 1: A Simple Case
Calculate the limit: lim (x→4) [(√x - 2) / (x - 4)]
- Identify the Radical: The radical expression is √x - 2.
- Determine the Conjugate: The conjugate is √x + 2.
- Multiply:
lim (x→4) [(√x - 2) / (x - 4)] * [(√x + 2) / (√x + 2)] = lim (x→4) [(x - 4) / ((x - 4)(√x + 2))] - Simplify: We can cancel (x - 4) from the numerator and denominator:
= lim (x→4) [1 / (√x + 2)] - Substitute: Substituting x = 4, we get:
= 1 / (√4 + 2) = 1 / 4
Therefore, lim (x→4) [(√x - 2) / (x - 4)] = 1/4.
Example 2: A More Complex Scenario
Calculate the limit: lim (x→∞) [(√(x² + 1) - x)]
- Identify the Radical: The radical expression is √(x² + 1).
- Determine the Conjugate: The conjugate is √(x² + 1) + x.
- Multiply:
lim (x→∞) [(√(x² + 1) - x) / 1] * [(√(x² + 1) + x) / (√(x² + 1) + x)] = lim (x→∞) [(x² + 1 - x²) / (√(x² + 1) + x)] = lim (x→∞) [1 / (√(x² + 1) + x)] - Simplify: As x approaches infinity, the denominator becomes very large, leading the entire expression to approach 0.
- Substitute:
= 0
Therefore, lim (x→∞) [(√(x² + 1) - x)] = 0.
Example 3: Dealing with Cube Roots
Calculate the limit: lim (x→0) [(∛x - 1) / (x -1)]
While this doesn't directly involve a square root, rationalization can be adapted. We can use the difference of cubes factorization: a³ - b³ = (a - b)(a² + ab + b²).
- Let a = ∛x and b = 1. Then a³ - b³ = x - 1.
- We can rewrite the expression as:
lim (x→0) [(∛x - 1) / ((∛x)³ - 1³)] - Apply the difference of cubes factorization:
lim (x→0) [(∛x - 1) / ((∛x - 1)((∛x)² + ∛x + 1))] - Simplify by canceling (∛x - 1):
lim (x→0) [1 / ((∛x)² + ∛x + 1)] - Substitute x = 0:
= 1 / (0 + 0 + 1) = 1
Therefore, lim (x→0) [(∛x - 1) / (x - 1)] = 1.
Advanced Techniques and Considerations
While the basic steps remain consistent, rationalization can become more involved with complex expressions. Here are some additional considerations:
- Multiple Radicals: If you encounter expressions with multiple radicals, you might need to apply the rationalization technique multiple times.
- Trigonometric Functions: Rationalization can be combined with trigonometric identities to solve limits involving trigonometric functions and radicals.
- L'Hôpital's Rule: For certain limits, especially those involving indeterminate forms like 0/0 or ∞/∞ where rationalization is difficult or impractical, L'Hôpital's Rule provides an alternative approach. However, rationalization is often simpler and more elegant when applicable.
Conclusion: Mastering Rationalization for Limit Calculations
Rationalization is a valuable tool in your calculus arsenal, allowing you to efficiently solve limits involving radicals. By mastering this technique, you'll be better equipped to tackle complex limit problems and gain a deeper understanding of limit evaluation strategies. Remember the key steps: identify the radical, find the conjugate, multiply, simplify, and substitute. Practice with various examples, gradually increasing the complexity, to build proficiency and confidence in your limit-solving abilities. Through consistent practice and a grasp of these principles, you'll navigate the world of limits with greater ease and accuracy.
Latest Posts
Latest Posts
-
How Many Cups Is 1 Pound Of Cheese
Jul 12, 2025
-
30 X 30 Is How Many Square Feet
Jul 12, 2025
-
How Much Does A Half Oz Weigh
Jul 12, 2025
-
Calories In An Omelette With 3 Eggs
Jul 12, 2025
-
How Do You Say Great Grandmother In Spanish
Jul 12, 2025
Related Post
Thank you for visiting our website which covers about How To Use Rationalizing To Calculating Limits . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.