In Jkl And Pqr If Jk Pq
Kalali
Jul 07, 2025 · 6 min read
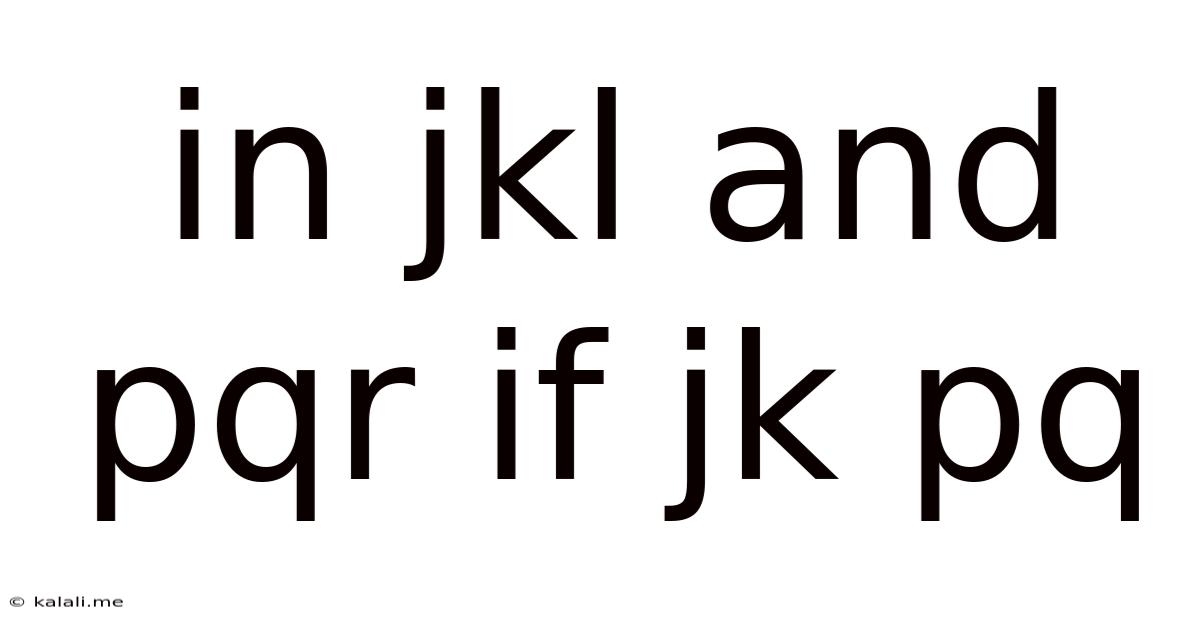
Table of Contents
Exploring the Relationship Between JK, PQ, and their Corresponding Geometrical Figures
This article delves into the implications of the statement "In JKL and PQR, if JK ≅ PQ," exploring its geometrical ramifications and the potential conclusions that can be drawn. We will unpack various scenarios, considering congruent triangles, similar triangles, and the broader context of geometric relationships within shapes. Understanding this fundamental concept is crucial for mastering geometry and solving complex problems.
Meta Description: This article comprehensively explores the geometric implications of JK ≅ PQ in triangles JKL and PQR, examining scenarios of congruence, similarity, and other potential relationships between the shapes. We cover various aspects of geometric proofs and problem-solving techniques.
Understanding Congruence and Similarity
Before diving into the specific relationship between triangles JKL and PQR based on JK ≅ PQ, it's crucial to understand the concepts of congruence and similarity.
Congruence: Two geometric figures are congruent if they have the same size and shape. In the context of triangles, this means that all corresponding sides and angles are equal. For triangles JKL and PQR to be congruent, we would need to demonstrate that:
- JK ≅ PQ
- KL ≅ QR
- LJ ≅ RP
- ∠J ≅ ∠P
- ∠K ≅ ∠Q
- ∠L ≅ ∠R
If only JK ≅ PQ, we cannot conclude that the triangles are congruent. We need additional information about the other sides or angles.
Similarity: Two geometric figures are similar if they have the same shape but not necessarily the same size. This means that corresponding angles are equal, and corresponding sides are proportional. For triangles JKL and PQR to be similar, we would need to show that:
- ∠J ≅ ∠P
- ∠K ≅ ∠Q
- ∠L ≅ ∠R
- JK/PQ = KL/QR = LJ/RP
Again, knowing only that JK ≅ PQ is insufficient to prove similarity. We require further information about angles or side ratios.
Scenarios Based on JK ≅ PQ
Let's explore different scenarios based solely on the information that JK ≅ PQ in triangles JKL and PQR.
Scenario 1: Insufficient Information
The most straightforward scenario is that knowing only JK ≅ PQ provides insufficient information to determine any definitive relationship between triangles JKL and PQR. They could be entirely different triangles with only one corresponding side of equal length. Numerous triangles can be constructed with a side of length equal to JK.
Scenario 2: Additional Information Required for Congruence
To prove congruence (△JKL ≅ △PQR), we need at least one additional piece of information. The possibilities include:
- Side-Side-Side (SSS): If we also know that KL ≅ QR and LJ ≅ RP, then by SSS congruence, we can conclude that △JKL ≅ △PQR.
- Side-Angle-Side (SAS): If we know that KL ≅ QR and ∠K ≅ ∠Q, then by SAS congruence, △JKL ≅ △PQR.
- Angle-Side-Angle (ASA): If we know that ∠J ≅ ∠P and ∠K ≅ ∠Q, then by ASA congruence, △JKL ≅ △PQR.
- Angle-Angle-Side (AAS): If we know that ∠J ≅ ∠P and ∠L ≅ ∠R, then by AAS congruence, △JKL ≅ △PQR.
Scenario 3: Additional Information Required for Similarity
Similarly, to prove similarity (△JKL ~ △PQR), we need additional information. The possibilities include:
- Side-Side-Side Similarity (SSS~): If the ratios of corresponding sides are equal (JK/PQ = KL/QR = LJ/RP), then the triangles are similar by SSS~.
- Side-Angle-Side Similarity (SAS~): If JK/PQ = KL/QR and ∠K ≅ ∠Q, then the triangles are similar by SAS~.
- Angle-Angle Similarity (AA~): If ∠J ≅ ∠P and ∠K ≅ ∠Q, then the triangles are similar by AA~. This is a particularly useful criterion because it requires only two angles to establish similarity.
Exploring Other Geometric Relationships
Beyond congruence and similarity, the knowledge that JK ≅ PQ in triangles JKL and PQR can open up the possibility of exploring other geometric relationships, albeit often requiring additional context or assumptions.
-
Isosceles Triangles: If, for example, we know that JK and KL are equal in △JKL (making it an isosceles triangle) and PQ and QR are equal in △PQR (also making it isosceles), then the equality of JK and PQ might be a part of a larger pattern indicating further relationships between the triangles' angles or other sides.
-
Specific Geometric Constructions: The condition JK ≅ PQ might be part of a larger geometrical problem where other constraints are given. This might lead to the triangles being part of a specific geometric construction, such as a rhombus, parallelogram, or a more complex figure. In such cases, the equality of JK and PQ could be a pivotal piece of information in determining properties of the overall geometric configuration.
-
Vector Geometry: In the context of vector geometry, the equality of JK and PQ could represent equal vectors. This means that the vectors representing the directed line segments JK and PQ have the same magnitude and direction. This could have implications in understanding the spatial relationships between points J, K, P, and Q.
-
Coordinate Geometry: If we are working in a coordinate system, the equality of JK and PQ might allow us to set up equations or inequalities that help us determine the coordinates of various points or the overall shape and properties of the figures.
Problem-Solving Strategies and Applications
Understanding the implications of JK ≅ PQ requires a systematic approach to problem-solving. Here's a structured approach:
-
Identify the Given Information: Clearly state that JK ≅ PQ.
-
Analyze the Context: Determine if there's any additional information provided about angles, sides, or the overall geometrical setup.
-
Explore Congruence Criteria: If sufficient information exists, apply the SSS, SAS, ASA, or AAS criteria to determine if the triangles are congruent.
-
Explore Similarity Criteria: If congruence cannot be established, apply the SSS~, SAS~, or AA~ criteria to check for similarity.
-
Consider Other Relationships: If neither congruence nor similarity can be definitively established, look for potential relationships such as isosceles triangles, or relationships within a larger geometric construction.
-
Visualization: Sketching the triangles can aid visualization and help identify potential relationships.
Conclusion
The statement "In JKL and PQR, if JK ≅ PQ" provides only a partial picture of the relationship between the two triangles. On its own, it's insufficient to prove congruence or similarity. To reach definitive conclusions about the relationship between △JKL and △PQR, additional information about the other sides or angles is necessary. The specific conclusions will depend entirely on the complete set of given information. By systematically analyzing the given information and applying appropriate geometric principles, we can accurately determine the relationship between these triangles. The ability to dissect such problems underscores the importance of a thorough understanding of geometric concepts and logical reasoning skills. Remember to always consider different scenarios and explore various geometric relationships, as the solution often lies in uncovering hidden connections.
Latest Posts
Latest Posts
-
How Long Can A Catfish Survive Out Of Water
Jul 07, 2025
-
Which Information Best Helps Portray Odysseus As A Heroic Archetype
Jul 07, 2025
-
How Long Does It Take To Drive 500 Miles
Jul 07, 2025
-
1880 Silver Dollar City Coin With Train
Jul 07, 2025
-
How Many 1 8 Tsp Are In 1 Tsp
Jul 07, 2025
Related Post
Thank you for visiting our website which covers about In Jkl And Pqr If Jk Pq . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.