Integral Of 1 X 4 1
Kalali
May 24, 2025 · 3 min read
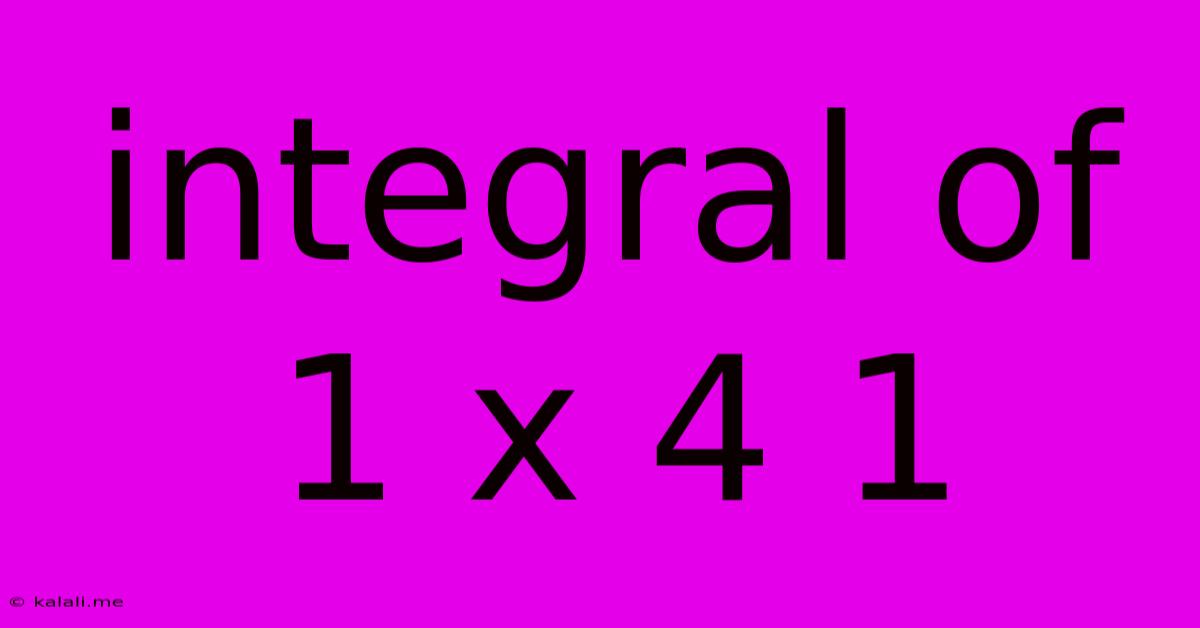
Table of Contents
Decoding the Integral: ∫1/(x⁴+1) dx
This article delves into the intriguing challenge of solving the indefinite integral ∫1/(x⁴+1) dx. This seemingly simple integral hides a surprising level of complexity, requiring a blend of algebraic manipulation, trigonometric substitution, and partial fraction decomposition to achieve a solution. Understanding this integral provides valuable insight into advanced integration techniques.
The integral ∫1/(x⁴+1) dx doesn't yield to simple u-substitution or straightforward integration rules. Its solution requires a multi-step approach that we'll unpack below. We'll explore the core concepts and steps, focusing on clarity and understanding rather than just presenting the final answer.
Step 1: Factoring the Denominator
The first crucial step involves factoring the denominator, x⁴ + 1. This quartic expression isn't easily factored using typical methods. However, we can factor it using a combination of techniques, ultimately leading to:
x⁴ + 1 = (x² + √2x + 1)(x² - √2x + 1)
This factorization is key to applying partial fraction decomposition in the subsequent steps. Understanding this factorization is crucial for solving many similar complex integrals. Note that the factors themselves are irreducible quadratic expressions.
Step 2: Partial Fraction Decomposition
With the denominator factored, we can now employ partial fraction decomposition. This technique allows us to break down the complex rational function into simpler fractions that are easier to integrate. The general form for this decomposition is:
1/(x⁴ + 1) = (Ax + B)/(x² + √2x + 1) + (Cx + D)/(x² - √2x + 1)
Finding the constants A, B, C, and D requires algebraic manipulation, usually involving equating coefficients after combining the fractions on the right-hand side. This process can be quite tedious but ultimately yields the values of these constants. (The actual calculation of A, B, C, and D is omitted here for brevity, but it's a standard algebraic procedure).
Step 3: Integrating the Partial Fractions
Once the partial fraction decomposition is complete, we're left with two integrals, each involving a fraction with an irreducible quadratic denominator. These integrals can be solved using a combination of techniques, often involving trigonometric substitution or completing the square followed by a standard integration formula for integrals involving quadratic expressions in the denominator.
For instance, you might encounter integrals of the form:
∫(Ax + B)/(x² + px + q) dx
which, after appropriate substitution and manipulation, can be solved using standard integration techniques. The specific substitutions and manipulations depend on the values of A, B, p, and q, which were determined in the previous step.
Step 4: Combining the Results
After solving the individual integrals from Step 3, the final step involves combining the results to obtain the complete solution for the original integral ∫1/(x⁴+1) dx. This will result in a rather lengthy expression involving logarithmic and arctangent functions. The exact form of this solution is complex and space-limiting to include in full here, but it is readily available through symbolic computation software such as Mathematica or Maple, or by consulting advanced calculus textbooks.
Conclusion: A Complex but Valuable Integral
The integral ∫1/(x⁴+1) dx serves as a powerful example of the sophisticated techniques needed to solve seemingly simple integrals. While the full solution is complex, understanding the underlying steps—factoring, partial fraction decomposition, and integration of the resulting fractions—provides valuable skills for tackling other challenging integrals encountered in advanced calculus and related fields. Remember, mastering these techniques involves practice and patience.
Latest Posts
Latest Posts
-
Kill Process Owned By User Over 10 Hours
May 24, 2025
-
Which Version Of Wind Waker Is Better
May 24, 2025
-
Var Spool Slurmd Job12662118 Slurm Script Line 136 Permem Unbound Variable
May 24, 2025
-
How To Say United States Of America In Spanish
May 24, 2025
-
Who Is The Angel Of Music
May 24, 2025
Related Post
Thank you for visiting our website which covers about Integral Of 1 X 4 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.