Integral X 2 1 X 4
Kalali
Jun 02, 2025 · 2 min read
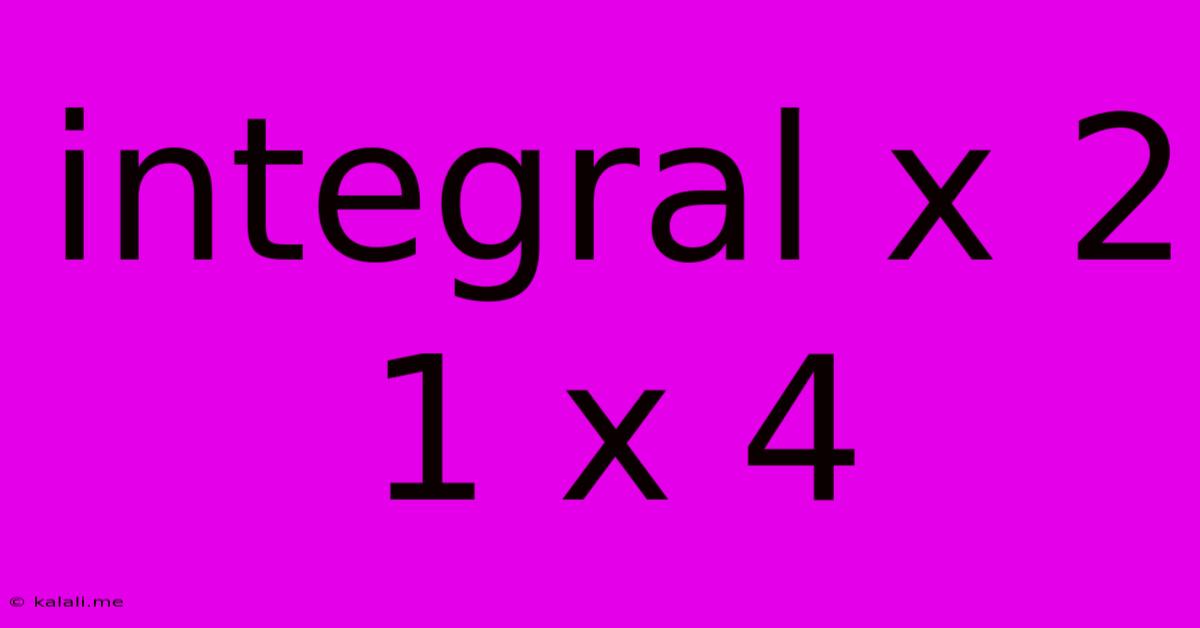
Table of Contents
Solving the Integral of x²/(1+x⁴)
This article will guide you through solving the definite integral ∫<sub>0</sub><sup>1</sup> x²/(1+x⁴) dx. This integral might seem daunting at first glance, but with the right approach, it becomes manageable. We'll explore several techniques and provide a step-by-step solution. Understanding this process will enhance your skills in calculus and integral calculations. This problem showcases the power of strategic substitution and trigonometric manipulation in integral calculus.
Understanding the Problem:
The integral ∫<sub>0</sub><sup>1</sup> x²/(1+x⁴) dx presents a challenge because the denominator is a quartic polynomial. Direct integration isn't immediately obvious. We need to employ a clever substitution to simplify the integrand.
Solving the Integral Using Substitution:
The key to solving this integral lies in a strategic substitution. Let's try substituting:
u = x²
This implies:
du = 2x dx or dx = du/(2√u)
Substituting this into the integral, we get:
∫ x²/(1+x⁴) dx = ∫ u/(1+u²) * (du/(2√u)) = (1/2) ∫ 1/(1+u²) du
This substitution transforms the integral into a much simpler form. The integral (1/2) ∫ 1/(1+u²) du is a standard integral that evaluates to:
(1/2) arctan(u) + C
Where 'C' is the constant of integration.
Back-Substitution and Definite Integral Evaluation:
Now, substitute back x² for u:
(1/2) arctan(x²) + C
To evaluate the definite integral from 0 to 1, we apply the limits of integration:
[(1/2) arctan(1²) ] - [(1/2) arctan(0²)] = (1/2) arctan(1) - (1/2) arctan(0)
Since arctan(1) = π/4 and arctan(0) = 0, the final result is:
(1/2) * (π/4) = π/8
Therefore, the definite integral ∫<sub>0</sub><sup>1</sup> x²/(1+x⁴) dx = π/8
Alternative Approaches (Advanced):
While the substitution method above is the most straightforward, other techniques could be applied, though they often involve more complex calculations. These might include partial fraction decomposition or trigonometric substitutions involving hyperbolic functions, but these are generally less efficient for this specific problem.
Conclusion:
Solving integrals like ∫<sub>0</sub><sup>1</sup> x²/(1+x⁴) dx requires a strategic approach and understanding of integral calculus techniques. This example highlights the importance of strategic substitution in simplifying complex integrals. By carefully selecting a substitution, we transformed a challenging integral into a readily solvable form, leading us to the solution of π/8. Mastering these techniques will build your confidence and efficiency in tackling similar problems in the future. Remember to always consider various methods and choose the most effective approach depending on the integrand's complexity.
Latest Posts
Latest Posts
-
What Size Is A 8 Screw
Jun 03, 2025
-
How To Clean Table Saw Metal Surface
Jun 03, 2025
-
Can I Upload Samples Of Songs On I Imusic
Jun 03, 2025
-
Dark Side Of The Moon Pictures
Jun 03, 2025
-
What To Do With Used Car Oil
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Integral X 2 1 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.