Integration Of X 2 A 2 1 2
Kalali
May 30, 2025 · 2 min read
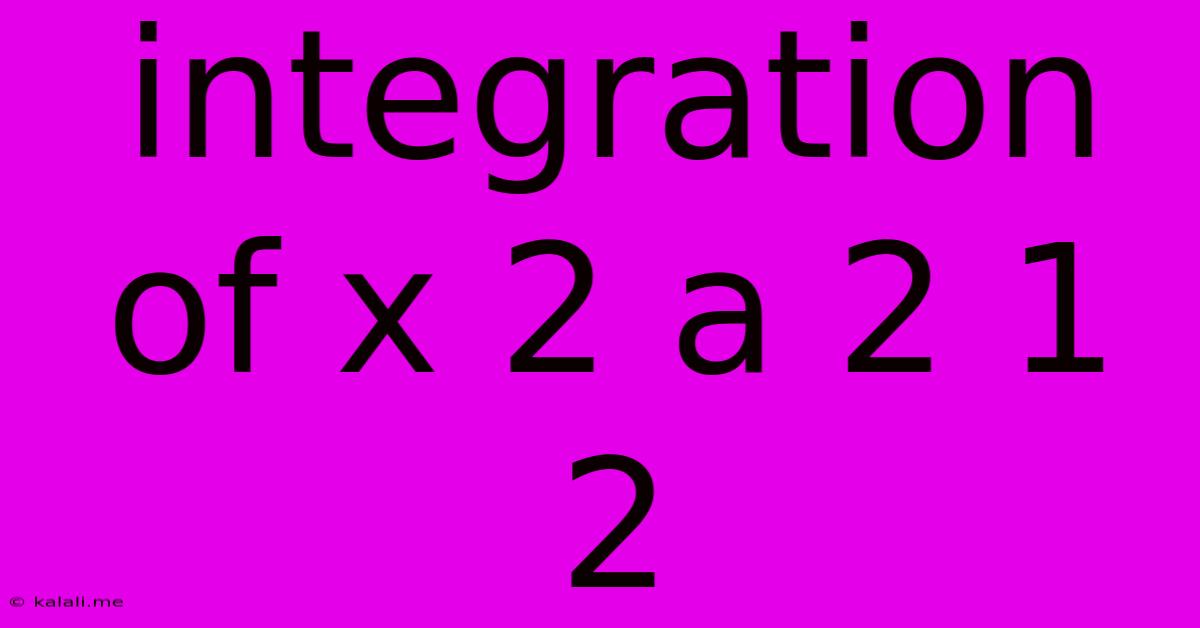
Table of Contents
The Integration of x²a² + 1/2: A Comprehensive Guide
This article explores the integration of the expression x²a² + 1/2, covering different approaches and highlighting key considerations. Understanding this integral is crucial for various applications in calculus, physics, and engineering. We'll break down the process step-by-step, ensuring a clear understanding for both beginners and those seeking a refresher.
Understanding the Problem
The integral we're tackling is ∫(x²a² + 1/2) dx. This involves finding the antiderivative of a polynomial expression containing a constant 'a'. The presence of 'a' adds a layer of complexity, requiring careful attention to constants during integration. We'll explore how to handle this constant effectively. The term '1/2' is a simple constant and will be easily integrated.
Step-by-Step Integration
The integration process follows the power rule of integration, which states that ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C, where 'n' is any real number except -1, and 'C' represents the constant of integration. Let's apply this rule to our expression:
-
Separate the terms: We can rewrite the integral as the sum of two separate integrals: ∫x²a² dx + ∫(1/2) dx. This simplifies the integration process.
-
Integrate the first term: Considering ∫x²a² dx, we treat 'a²' as a constant. Applying the power rule, we get: (a²(x³)/3) + C₁. Notice how the constant 'a²' remains unchanged throughout the integration.
-
Integrate the second term: Integrating ∫(1/2) dx is straightforward. The antiderivative of a constant is the constant multiplied by x: (1/2)x + C₂.
-
Combine the results: Combining the results from steps 2 and 3, and consolidating the constants of integration (C₁ + C₂ = C), we get the final solution: (a²(x³)/3) + (1/2)x + C.
Key Considerations and Applications
-
The Constant 'a': Remember that 'a' is treated as a constant throughout the integration process. Its value is not determined by the integration itself; it must be known or given beforehand.
-
Constant of Integration (C): The constant of integration 'C' is crucial. It represents a family of antiderivatives, each differing by a constant value. Its presence is essential for a complete and accurate solution.
-
Applications: Integrals like this have diverse applications. In physics, they could describe displacement given acceleration, or in engineering, they might be used in calculating areas under curves or volumes of revolution.
Conclusion
Integrating x²a² + 1/2 is a fundamental exercise in calculus, demonstrating the application of the power rule and highlighting the importance of correctly handling constants. By carefully applying the power rule and combining the results, we've successfully found the antiderivative. Remember the key considerations regarding the constant 'a' and the constant of integration 'C' to ensure accurate solutions in your own calculations. This understanding forms a base for tackling more complex integration problems in the future.
Latest Posts
Latest Posts
-
How To Get Water Stain Out Of Wood
May 31, 2025
-
Why Does My Yorkie Have Green Eyes
May 31, 2025
-
What Does Open Ground Mean In Electrical
May 31, 2025
-
How To Strip A Painted Deck
May 31, 2025
-
How To Get Bugs Out Of Raspberries
May 31, 2025
Related Post
Thank you for visiting our website which covers about Integration Of X 2 A 2 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.