Integration Of X 2e X 2
Kalali
Jun 01, 2025 · 3 min read
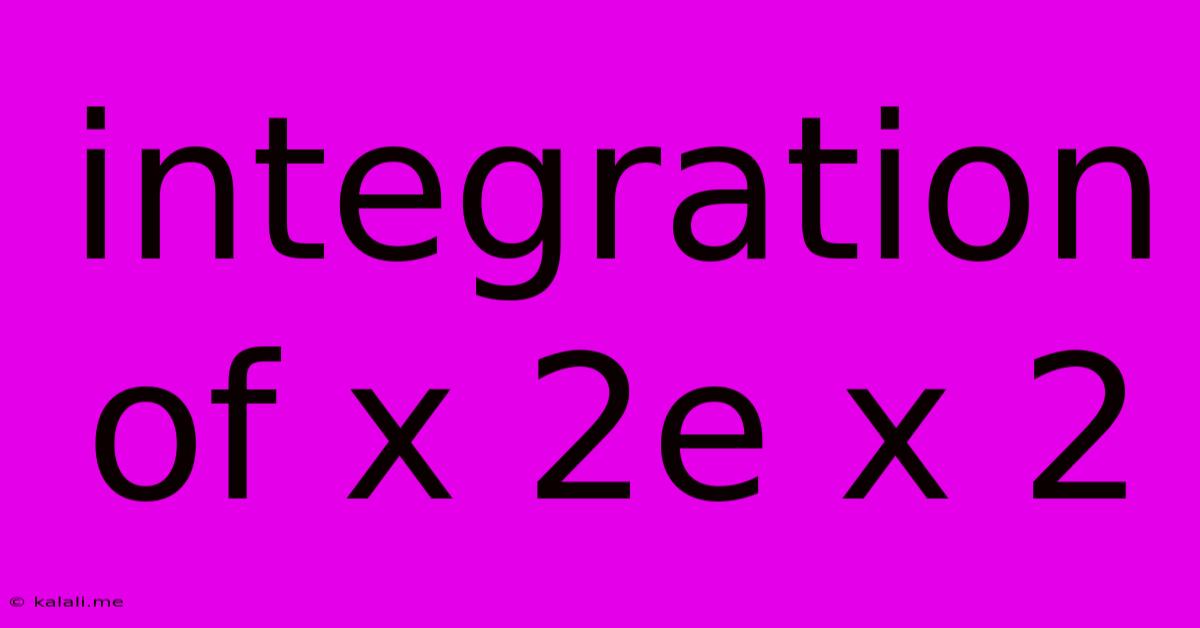
Table of Contents
Mastering the Integration of x²eˣ²: A Comprehensive Guide
This article provides a detailed walkthrough of integrating x²eˣ², a problem frequently encountered in calculus. We'll explore various methods, highlighting their strengths and weaknesses, ultimately equipping you with the skills to tackle similar integration problems. Understanding this integration technique will enhance your calculus skills significantly, making you more confident in solving complex mathematical problems.
Integrating x²eˣ² isn't directly solvable using standard integration rules. Therefore, we'll need to employ a more sophisticated technique: integration by parts. This powerful method leverages the product rule of differentiation to solve integrals involving products of functions.
Understanding Integration by Parts
The formula for integration by parts is: ∫u dv = uv - ∫v du
The key to success lies in strategically choosing 'u' and 'dv'. A useful mnemonic is LIATE:
- Logarithmic functions
- Inverse trigonometric functions
- Algebraic functions (like x²)
- Trigonometric functions
- Exponential functions
This order suggests prioritizing logarithmic functions for 'u' if present, then inverse trigonometric, and so on.
Applying Integration by Parts to x²eˣ²
Let's apply integration by parts to ∫x²eˣ² dx.
-
Choose u and dv: Following LIATE, we choose:
- u = x² => du = 2x dx
- dv = eˣ² dx => v = This is where it gets tricky. There's no elementary antiderivative for eˣ².
This highlights a limitation of the straightforward application of integration by parts in this case. The choice of 'dv' leads to a non-elementary integral.
Alternative Approaches and Advanced Techniques
Because a direct application of integration by parts fails, we need to consider alternative approaches or advanced techniques. This integral, in its presented form, doesn't have a closed-form solution using elementary functions. This doesn't mean it's unsolvable, just that the solution involves special functions or numerical methods.
1. Numerical Integration: Techniques like the Trapezoidal Rule or Simpson's Rule can provide approximate solutions for definite integrals. These methods are computationally efficient and yield good approximations for many integrals, particularly those lacking elementary antiderivatives.
2. Series Expansion: The integrand, x²eˣ², can be expressed as a power series using the Taylor series expansion of eˣ. Integrating the resulting power series term-by-term can give an approximation of the integral, offering a solution in terms of an infinite series. The accuracy depends on the number of terms included in the approximation.
3. Special Functions: Certain integrals involving exponential functions and polynomials sometimes lead to solutions expressed using special functions, like the error function (erf) or other related functions. These functions are defined by integrals and aren't elementary functions themselves. Therefore, it is unlikely you will need to utilize special functions to integrate x²eˣ² unless you are in an advanced mathematical context.
Conclusion
While a simple, closed-form solution for ∫x²eˣ² dx using standard integration techniques isn't possible, alternative methods provide ways to evaluate the integral. Numerical integration offers approximate solutions for definite integrals, while power series expansions or special functions might provide solutions in different forms. The best approach depends on the specific context and the level of accuracy required. Understanding these different approaches broadens your problem-solving skills in calculus and enhances your ability to tackle complex integrals. Remember to carefully consider the properties of the integrand when selecting an appropriate integration method.
Latest Posts
Latest Posts
-
How To Know Head Gasket Is Blown
Jun 03, 2025
-
Is A Periodical Title A Magazine Title
Jun 03, 2025
-
Many Are Called But Few Are Chosen Meaning
Jun 03, 2025
-
How To Change Bulb On Recessed Light
Jun 03, 2025
-
Can Stainless Steel Cookware Go In The Oven
Jun 03, 2025
Related Post
Thank you for visiting our website which covers about Integration Of X 2e X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.