Is 1 2 Bigger Than 1 8
Kalali
Jul 28, 2025 · 5 min read
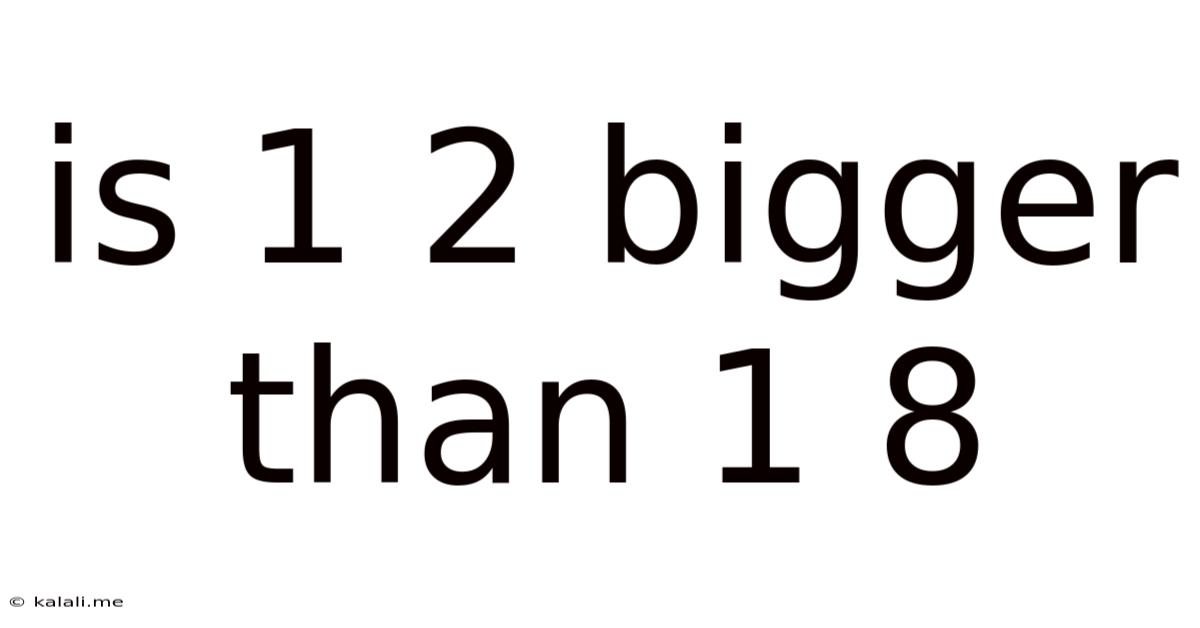
Table of Contents
Is 1/2 Bigger Than 1/8? A Deep Dive into Fractions and Comparisons
This seemingly simple question, "Is 1/2 bigger than 1/8?", opens the door to a fascinating exploration of fractions, their representation, and various methods for comparing them. While the answer might seem obvious to some, understanding the underlying principles is crucial for anyone looking to grasp fundamental mathematical concepts and improve their problem-solving skills. This article will delve into the comparison of these fractions, providing multiple approaches to confirm the answer and exploring broader concepts related to fraction comparison and mathematical reasoning.
Meta Description: This comprehensive guide explores the comparison of fractions 1/2 and 1/8, explaining various methods to determine which is larger and exploring fundamental concepts related to fractions and mathematical reasoning. Learn about visual representations, equivalent fractions, and decimal conversions.
Understanding Fractions: Parts of a Whole
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
In our case, 1/2 means we have 1 part out of a total of 2 equal parts, while 1/8 means we have 1 part out of a total of 8 equal parts. Visualizing this is often the easiest way to understand the difference.
Visual Representation: The Power of Pictures
Imagine a pizza cut into two equal slices (1/2) and another pizza cut into eight equal slices (1/8). If you take one slice from the first pizza (1/2), you'll have a significantly larger piece compared to taking one slice from the second pizza (1/8). This visual representation clearly demonstrates that 1/2 is larger than 1/8. This method is particularly useful for beginners as it offers an intuitive understanding of fractional magnitudes. Other visual aids, like fraction bars or circles divided into segments, can also effectively illustrate this concept.
Equivalent Fractions: Finding Common Ground
Another approach to comparing fractions is to find equivalent fractions with a common denominator. This involves converting both fractions into forms that share the same denominator. Finding the least common multiple (LCM) of the denominators (2 and 8) is helpful. The LCM of 2 and 8 is 8.
- We can convert 1/2 to an equivalent fraction with a denominator of 8 by multiplying both the numerator and denominator by 4: (1 x 4) / (2 x 4) = 4/8
Now we can easily compare 4/8 and 1/8. Since 4/8 has a larger numerator than 1/8, it represents a larger portion of the whole. Therefore, 1/2 (which is equal to 4/8) is larger than 1/8.
Decimal Conversion: A Numerical Approach
Converting fractions to decimals provides another way to compare them. To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 1/2 = 1 ÷ 2 = 0.5
- 1/8 = 1 ÷ 8 = 0.125
Comparing the decimal values, 0.5 is clearly larger than 0.125. This method reinforces the fact that 1/2 is bigger than 1/8. This approach is useful for those comfortable with decimal representations and allows for easy comparison using a numerical scale.
Cross-Multiplication: A Direct Comparison Method
Cross-multiplication offers a direct method for comparing fractions. This involves multiplying the numerator of one fraction by the denominator of the other, and vice versa. The larger product corresponds to the larger fraction.
- Cross-multiply 1/2 and 1/8:
- 1 (numerator of 1/2) x 8 (denominator of 1/8) = 8
- 1 (numerator of 1/8) x 2 (denominator of 1/2) = 2
Since 8 > 2, the fraction 1/2 is larger than 1/8. This technique is efficient and avoids the need for finding a common denominator or converting to decimals, making it a powerful tool in fraction comparison.
Number Line Representation: Visualizing Magnitude
A number line provides a visual representation of the relative magnitudes of numbers, including fractions. Plotting 1/2 and 1/8 on a number line clearly shows that 1/2 is located further to the right, indicating its larger value. This method offers a spatial understanding of the relationship between fractions.
Extending the Concept: Comparing More Complex Fractions
The principles discussed above can be applied to comparing more complex fractions. For example, consider comparing 3/4 and 5/8. Using equivalent fractions, we can convert 3/4 to 6/8. Since 6/8 > 5/8, we can conclude that 3/4 is larger than 5/8. The same methods of decimal conversion and cross-multiplication can also be employed. The key is to systematically apply the chosen method to ensure accurate comparison.
Real-World Applications: Fractions in Everyday Life
Understanding fraction comparison is essential in many real-world scenarios. From cooking and baking (measuring ingredients) to construction (precise measurements) and finance (calculating proportions and percentages), the ability to accurately compare fractions is crucial for accurate and effective problem-solving. Consider situations where you need to compare different discounts, share resources fairly, or understand proportions in various contexts. Mastering fraction comparison empowers you to navigate these scenarios with confidence.
Conclusion: A Solid Foundation in Fractions
The simple question, "Is 1/2 bigger than 1/8?" serves as a gateway to a deeper understanding of fractions. By exploring various methods of comparison – visual representation, equivalent fractions, decimal conversion, cross-multiplication, and number line representation – we've established a solid foundation for comparing fractions of any complexity. The ability to confidently compare fractions is a fundamental skill that transcends mathematical exercises, finding practical application in diverse real-world situations. Mastering these techniques equips you with a valuable tool for solving problems and making informed decisions in various aspects of life. Further exploration into fraction operations (addition, subtraction, multiplication, and division) will build upon this foundational knowledge, allowing you to confidently tackle more complex mathematical problems.
Latest Posts
Latest Posts
-
How Much Does 5 Gallons Of Dirt Weigh
Jul 29, 2025
-
How Far Is 10 Miles In Minutes Driving
Jul 29, 2025
-
How Many Cups Are In 90 Grams
Jul 29, 2025
-
How Fast Is 299 Km In Mph
Jul 29, 2025
-
How Far Is Alaska From Washington State
Jul 29, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Bigger Than 1 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.