Is 1 2 Greater Than 3 5
Kalali
Jul 21, 2025 · 4 min read
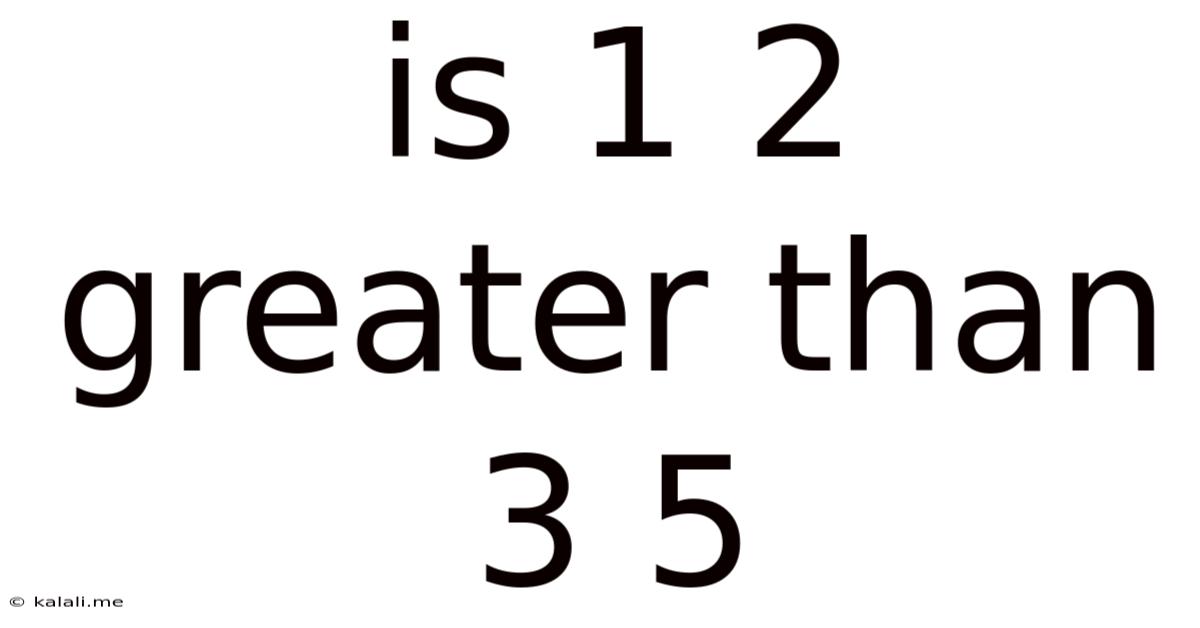
Table of Contents
Is 1/2 Greater Than 3/5? A Deep Dive into Fraction Comparison
This article will explore the question: "Is 1/2 greater than 3/5?" This seemingly simple question provides a great opportunity to delve into the fundamentals of fraction comparison, offering a comprehensive understanding for students and a refresher for those needing to brush up on their math skills. We will cover various methods for comparing fractions, including finding common denominators, converting to decimals, and using cross-multiplication. We'll also explore the broader context of rational numbers and their representation. Understanding fraction comparison is crucial for various mathematical operations and real-world applications.
Understanding Fractions: A Quick Review
Before we tackle the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two main parts:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For instance, in the fraction 1/2, the numerator (1) represents one part, and the denominator (2) means the whole is divided into two equal parts.
Method 1: Finding a Common Denominator
This is perhaps the most common and conceptually straightforward method. To compare fractions, we need to rewrite them with the same denominator. This allows for direct comparison of the numerators.
To find a common denominator for 1/2 and 3/5, we look for the least common multiple (LCM) of 2 and 5. The LCM of 2 and 5 is 10.
We then rewrite each fraction with a denominator of 10:
- 1/2 = (1 * 5) / (2 * 5) = 5/10
- 3/5 = (3 * 2) / (5 * 2) = 6/10
Now, comparing the numerators, we see that 5/10 < 6/10. Therefore, 1/2 < 3/5.
Method 2: Converting to Decimals
Another effective method is to convert the fractions into their decimal equivalents. This is particularly useful when dealing with more complex fractions or when a decimal representation is needed for practical applications.
To convert a fraction to a decimal, we simply divide the numerator by the denominator:
- 1/2 = 1 ÷ 2 = 0.5
- 3/5 = 3 ÷ 5 = 0.6
Comparing the decimal equivalents, we find that 0.5 < 0.6. Again, this confirms that 1/2 < 3/5.
Method 3: Cross-Multiplication
Cross-multiplication provides a more efficient way to compare fractions, especially when dealing with larger numbers or fractions that are difficult to find a common denominator for.
To use cross-multiplication, we multiply the numerator of the first fraction by the denominator of the second fraction, and vice versa. We then compare the products.
For 1/2 and 3/5:
- (1 * 5) = 5
- (2 * 3) = 6
Since 5 < 6, we conclude that 1/2 < 3/5. This method directly compares the relative sizes of the fractions without the need for finding a common denominator.
Visual Representation: Understanding Fraction Size
Visualizing fractions can greatly aid in understanding their relative sizes. Imagine two identical pizzas. One is cut into two equal slices, and you take one slice (1/2). The other is cut into five equal slices, and you take three slices (3/5). Visually comparing the amount of pizza you have in each case clearly shows that 3/5 is larger than 1/2.
Expanding the Concept: Rational Numbers and Their Ordering
Fractions belong to a larger set of numbers called rational numbers. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. Understanding the comparison of fractions is fundamental to understanding the ordering of rational numbers on the number line.
Real-World Applications: Where Fraction Comparison Matters
The ability to compare fractions is crucial in numerous real-world scenarios:
- Baking: Following recipes often requires comparing fractions of ingredients.
- Construction: Measuring materials and distances frequently involves fractions.
- Finance: Calculating portions of budgets, interest rates, and loan payments necessitates fraction comparison.
- Data Analysis: Understanding proportions and percentages, which are essentially fractions, is essential in interpreting data.
Beyond Simple Fractions: Dealing with Mixed Numbers and Improper Fractions
The methods described above can be extended to compare mixed numbers (a whole number and a fraction) and improper fractions (where the numerator is larger than the denominator). In these cases, it's often helpful to convert the mixed numbers or improper fractions into improper fractions before applying the comparison methods.
Advanced Techniques: Using Number Lines and Proportions
For a more visual approach, you can plot the fractions on a number line. This visually demonstrates their relative positions and sizes. Furthermore, the concept of proportions can be used to establish relationships between fractions and compare them indirectly.
Conclusion: Mastering Fraction Comparison
The question "Is 1/2 greater than 3/5?" serves as a springboard to understand the core concepts of fraction comparison. We've explored multiple methods—finding a common denominator, converting to decimals, and cross-multiplication—providing a versatile toolkit for tackling various fraction comparison problems. Remember, visualizing fractions, understanding rational numbers, and recognizing real-world applications solidify the understanding and make fraction comparison an intuitive and essential skill. By mastering these techniques, you'll build a strong foundation for more advanced mathematical concepts and real-world problem-solving. The answer, definitively, is no; 1/2 is less than 3/5. Understanding why is the key takeaway.
Latest Posts
Latest Posts
-
What Is Another Way To Get 19
Jul 21, 2025
-
Why Does S E Hinton Use Her Initials
Jul 21, 2025
-
How Do I Say Hello In Swahili
Jul 21, 2025
-
What Is The Number In Front Of A Variable Called
Jul 21, 2025
-
What Is The Meaning Of The Prefix Dyn
Jul 21, 2025
Related Post
Thank you for visiting our website which covers about Is 1 2 Greater Than 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.