Is 2 3 Greater Than 2 4
Kalali
Jun 30, 2025 · 5 min read
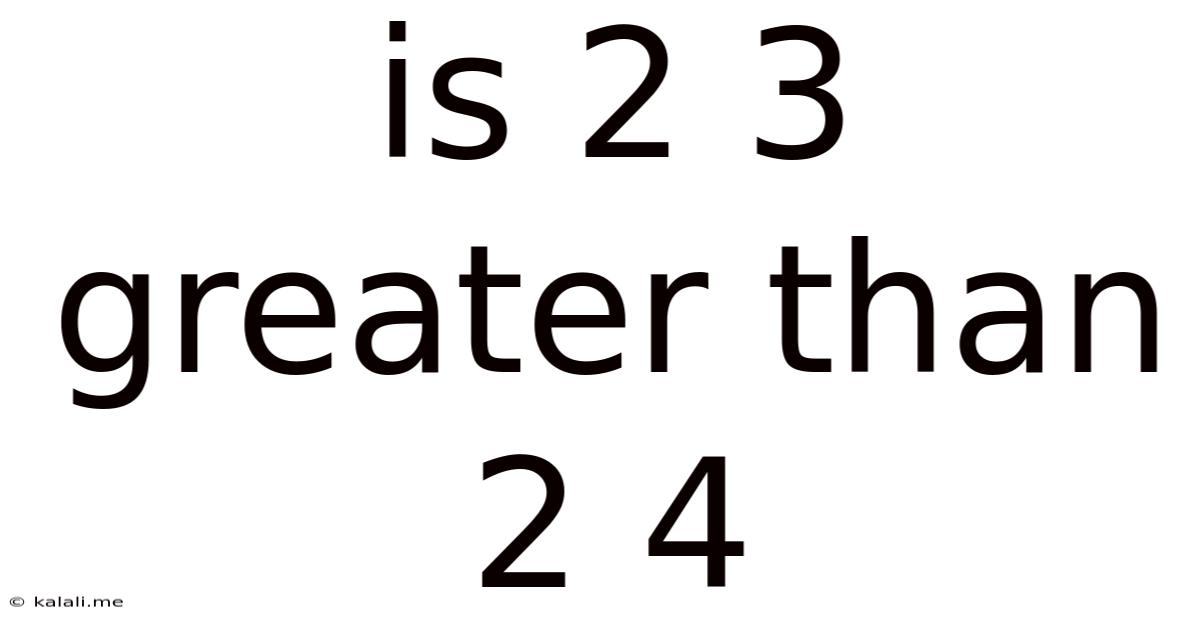
Table of Contents
Is 2³ Greater Than 2⁴? Understanding Exponential Growth and Number Comparisons
This seemingly simple question, "Is 2³ greater than 2⁴?", opens the door to a deeper understanding of exponential growth, a fundamental concept in mathematics with wide-ranging applications in various fields like finance, science, and computer science. This article will not only answer the question definitively but also explore the underlying principles, provide practical examples, and discuss how to compare numbers expressed in exponential form.
Meta Description: Learn the answer to "Is 2³ greater than 2⁴?" and explore the world of exponential growth. This comprehensive guide explains exponents, compares exponential numbers, and provides real-world applications to solidify your understanding.
The short answer is no, 2³ is not greater than 2⁴. However, understanding why requires a grasp of exponential notation and how it represents repeated multiplication.
Understanding Exponents
An exponent, also known as a power or index, indicates how many times a number (the base) is multiplied by itself. In the expression a<sup>b</sup>, 'a' is the base, and 'b' is the exponent. This means 'a' is multiplied by itself 'b' times.
Let's break down our example:
- 2³ (two cubed or two to the power of three): This means 2 × 2 × 2 = 8
- 2⁴ (two to the power of four): This means 2 × 2 × 2 × 2 = 16
Therefore, 8 (2³) is smaller than 16 (2⁴).
Comparing Exponential Numbers
Comparing numbers expressed with exponents requires understanding the relationship between the base and the exponent. Several scenarios can arise:
1. Same Base, Different Exponents:
When comparing numbers with the same base but different exponents, the number with the larger exponent will always be greater (assuming the base is greater than 1). This is because each increment in the exponent represents an additional multiplication by the base.
For instance:
- 3² < 3³ < 3⁴ (9 < 27 < 81)
- 10¹ < 10² < 10³ (10 < 100 < 1000)
2. Different Bases, Same Exponent:
When comparing numbers with different bases but the same exponent, the number with the larger base will be greater (assuming the exponent is greater than 0).
For example:
- 2³ < 3³ < 4³ (8 < 27 < 64)
- 5² < 6² < 7² (25 < 36 < 49)
3. Different Bases and Different Exponents:
This scenario requires a bit more calculation. The simplest approach is to calculate the values of both expressions and then compare the results. However, for larger numbers, logarithmic functions can be used for comparison.
Example:
Is 5³ greater than 2⁵?
- 5³ = 5 × 5 × 5 = 125
- 2⁵ = 2 × 2 × 2 × 2 × 2 = 32
Therefore, 5³ > 2⁵.
Real-World Applications of Exponential Growth
Exponential growth is not just a mathematical concept; it's a powerful tool for modeling real-world phenomena:
1. Compound Interest: The growth of money invested with compound interest follows an exponential pattern. The interest earned each period is added to the principal, and subsequent interest calculations are based on the larger amount. This leads to significantly faster growth compared to simple interest.
2. Population Growth: Under ideal conditions, the population of many species exhibits exponential growth. Each organism reproduces, adding to the population, and those offspring also reproduce, leading to a rapid increase in numbers. However, factors like resource limitations and environmental constraints often limit this exponential growth.
3. Bacterial Growth: The growth of bacterial colonies under ideal conditions also demonstrates exponential growth. Each bacterium divides into two, doubling the population, and this process repeats rapidly.
4. Viral Spread: The spread of infectious diseases, especially in the early stages of an epidemic, can be modeled using exponential functions. Each infected individual can potentially infect multiple others, leading to an exponential increase in the number of cases. This highlights the importance of early intervention and preventative measures.
5. Radioactive Decay: While not strictly growth, radioactive decay follows an exponential decay function. The amount of radioactive material decreases exponentially over time, with a constant half-life. This is crucial for understanding nuclear physics and managing radioactive waste.
6. Computer Science: Exponential functions are critical in computer science, particularly in analyzing algorithm efficiency. Some algorithms have exponential time complexity, meaning their execution time grows exponentially with the size of the input data. This can lead to extremely long processing times for even moderately sized inputs. Understanding this is vital for optimizing software performance.
Beyond 2³ and 2⁴: Exploring Larger Exponents
While the comparison of 2³ and 2⁴ is straightforward, understanding how exponents work becomes even more critical when dealing with larger numbers. Consider the following:
- 2¹⁰ (two to the power of ten): This equals 1024. This shows how quickly exponential growth can lead to substantial numbers.
- Comparing 10² and 2¹⁰: While the bases are different, the exponents aren't too far apart. But 10² (100) is significantly smaller than 2¹⁰ (1024). This again highlights the impact of both the base and the exponent.
Understanding these relationships is crucial for tasks such as:
- Data analysis: Identifying exponential trends in datasets
- Scientific modeling: Creating accurate simulations of processes governed by exponential growth or decay
- Financial planning: Accurately projecting future values of investments
Advanced Techniques for Comparing Exponential Numbers
For more complex comparisons involving large numbers or different bases and exponents, more advanced mathematical techniques can be used. These include:
- Logarithms: Logarithms are the inverse of exponents. Taking the logarithm of exponential numbers can simplify comparisons, allowing for easier assessment of relative magnitudes.
- Numerical approximation: For very large numbers, numerical methods may be necessary to approximate values and facilitate comparisons. Software tools and calculators can be incredibly helpful in this regard.
Conclusion: Mastering Exponential Growth for Practical Applications
The seemingly simple question, "Is 2³ greater than 2⁴?", serves as a springboard to explore the fascinating world of exponential growth. Understanding exponential notation, comparing exponential numbers, and recognizing the real-world applications of this fundamental concept are essential skills for anyone working with data, models, or any field involving significant growth or decay. By mastering these principles, you'll be better equipped to interpret data, solve problems, and make informed decisions across numerous disciplines. Remember that while simple examples like 2³ and 2⁴ are easily calculated, the principles discussed here extend to far more complex scenarios and are indispensable in many professional and academic fields.
Latest Posts
Latest Posts
-
How Many Ounces Are In A Key
Jun 30, 2025
-
How Old Am I If I Was Born 1969
Jun 30, 2025
-
2 Bottles Of 750ml Equals How Many Liters
Jun 30, 2025
-
How Many Seconds Are In 100 Years
Jun 30, 2025
-
How Old Is Someone Born In 1969
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Greater Than 2 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.