Is 2 3 Greater Than 5 8
Kalali
Jul 26, 2025 · 5 min read
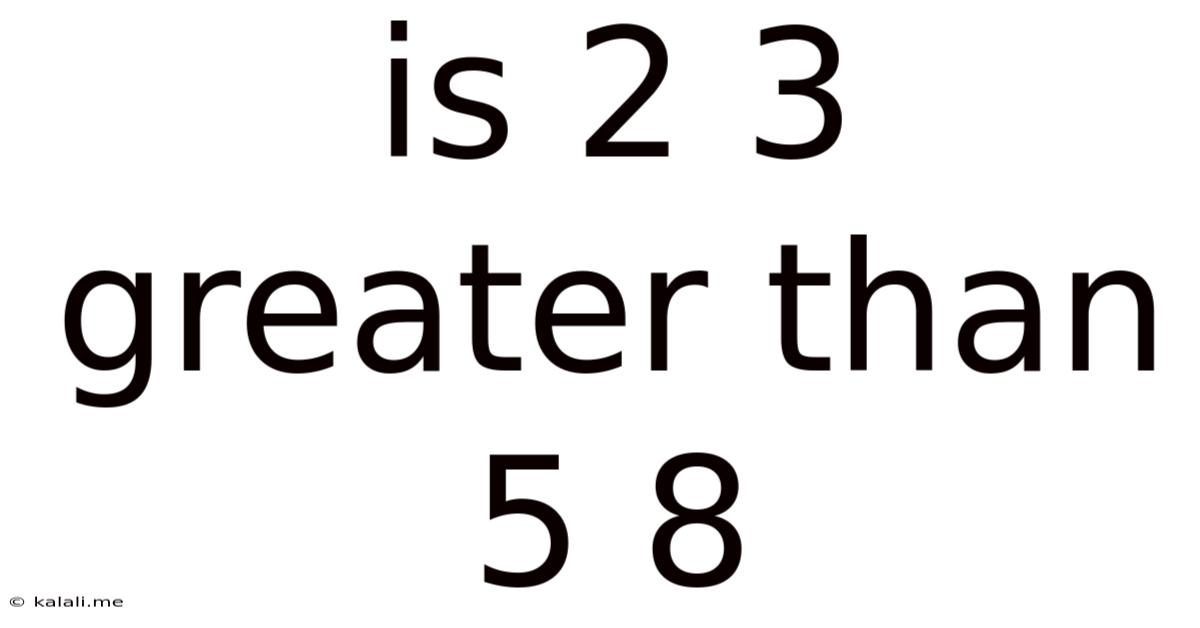
Table of Contents
Is 2/3 Greater Than 5/8? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 2/3 greater than 5/8?", opens a door to a deeper understanding of fractions, their representation, and various methods for comparing them. While the answer itself is straightforward once you employ the right technique, the process reveals fundamental concepts in mathematics crucial for various applications, from basic arithmetic to advanced calculus. This article will not only answer the question definitively but also explore several approaches to comparing fractions, highlighting their strengths and weaknesses. This will equip you with the tools to confidently tackle similar comparisons in the future.
Meta Description: Learn how to compare fractions effectively! This comprehensive guide explains multiple methods for determining whether 2/3 is greater than 5/8, covering decimal conversion, finding common denominators, and cross-multiplication. Master fraction comparison and boost your math skills.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's briefly review what fractions represent. A fraction, like 2/3, consists of two parts: the numerator (the top number, 2 in this case) and the denominator (the bottom number, 3). The numerator indicates the number of parts we have, while the denominator indicates the total number of equal parts the whole is divided into. Therefore, 2/3 represents two out of three equal parts of a whole.
Similarly, 5/8 represents five out of eight equal parts of a whole. Understanding this fundamental concept is key to comparing fractions effectively.
Method 1: Converting to Decimals
One of the simplest approaches to comparing fractions is converting them into decimal numbers. This method relies on dividing the numerator by the denominator.
- 2/3 as a decimal: 2 ÷ 3 ≈ 0.6667 (repeating decimal)
- 5/8 as a decimal: 5 ÷ 8 = 0.625
By converting both fractions to decimals, we can clearly see that 0.6667 is greater than 0.625. Therefore, 2/3 is greater than 5/8.
This method is intuitive and easy to understand, especially with the aid of a calculator. However, it's important to note that repeating decimals, like the one for 2/3, can introduce slight inaccuracies depending on the level of decimal precision used.
Method 2: Finding a Common Denominator
This classic method involves finding a common denominator for both fractions, allowing for a direct comparison of the numerators. The common denominator is a multiple of both denominators.
-
Find the least common multiple (LCM) of 3 and 8: The LCM of 3 and 8 is 24.
-
Rewrite the fractions with the common denominator:
- 2/3 = (2 × 8) / (3 × 8) = 16/24
- 5/8 = (5 × 3) / (8 × 3) = 15/24
-
Compare the numerators: Since 16 > 15, we conclude that 16/24 (or 2/3) is greater than 15/24 (or 5/8).
This method provides an exact comparison, avoiding any potential inaccuracies associated with decimal approximations. However, finding the LCM can be challenging for larger denominators, requiring knowledge of prime factorization or other techniques.
Method 3: Cross-Multiplication
This efficient method involves multiplying the numerator of one fraction by the denominator of the other and vice-versa. Comparing the resulting products determines which fraction is larger.
-
Cross-multiply:
- 2 × 8 = 16
- 5 × 3 = 15
-
Compare the products: Since 16 > 15, we conclude that 2/3 is greater than 5/8.
Cross-multiplication offers a quick and accurate method for comparing fractions, eliminating the need for finding a common denominator. It’s a particularly useful technique for larger fractions where finding the LCM might be time-consuming.
Method 4: Visual Representation
While less precise for complex fractions, visualizing the fractions using diagrams or models can offer a clear understanding of their relative sizes. Imagine two identical circles. Divide one circle into three equal parts and shade two of them (representing 2/3). Divide the other circle into eight equal parts and shade five of them (representing 5/8). A visual comparison will readily show that the shaded area in the 2/3 circle is larger.
Choosing the Best Method
The optimal method for comparing fractions depends on the context and the complexity of the fractions involved.
- For simple fractions and quick comparisons: Decimal conversion or cross-multiplication are efficient choices.
- For fractions requiring precise comparison and avoiding decimal approximations: Finding a common denominator is the preferred method.
- For introductory understanding or visual learners: Visual representations provide a helpful starting point.
Extending the Concept: Comparing More Than Two Fractions
The methods discussed above can be extended to compare more than two fractions. For instance, to compare 2/3, 5/8, and 7/12, you can utilize any of the methods—decimal conversion, common denominator, or cross-multiplication—but you'll need to apply them systematically to each pair of fractions. Finding a common denominator for all three fractions is the most straightforward approach in this scenario.
Applications in Real-World Scenarios
The ability to compare fractions is not limited to mathematical exercises; it has practical applications in various fields:
- Baking: Following recipes accurately often requires understanding and comparing fractional measurements of ingredients.
- Construction: Precise measurements in construction projects frequently involve fractions.
- Finance: Calculating interest rates, proportions, and shares often requires fraction manipulation.
- Data Analysis: Understanding and representing data proportions involves working with fractions.
Conclusion: Mastering Fraction Comparison
The question, "Is 2/3 greater than 5/8?", serves as a springboard for exploring fundamental concepts in fraction comparison. Mastering these methods—decimal conversion, finding common denominators, and cross-multiplication—equips you with crucial skills applicable in various mathematical contexts and real-world situations. Remember to choose the method best suited to the specific problem, prioritizing accuracy and efficiency. By understanding the underlying principles of fractions, you can navigate complex mathematical problems with confidence and precision. Practice regularly, and you'll soon find comparing fractions to be a straightforward task. This ability will enhance your problem-solving skills and broaden your understanding of the mathematical world.
Latest Posts
Latest Posts
-
How Long Can Milk Stay In The Car
Jul 26, 2025
-
You Make Me Smile Please Stay For A While
Jul 26, 2025
-
Is Firetruck One Word Or Two Words
Jul 26, 2025
-
Is Eric Close The Son Of Glenn Close
Jul 26, 2025
-
How Many Miles Are In 8800 Yards
Jul 26, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 Greater Than 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.