Is 2 3 More Than 1 2
Kalali
Jun 30, 2025 · 4 min read
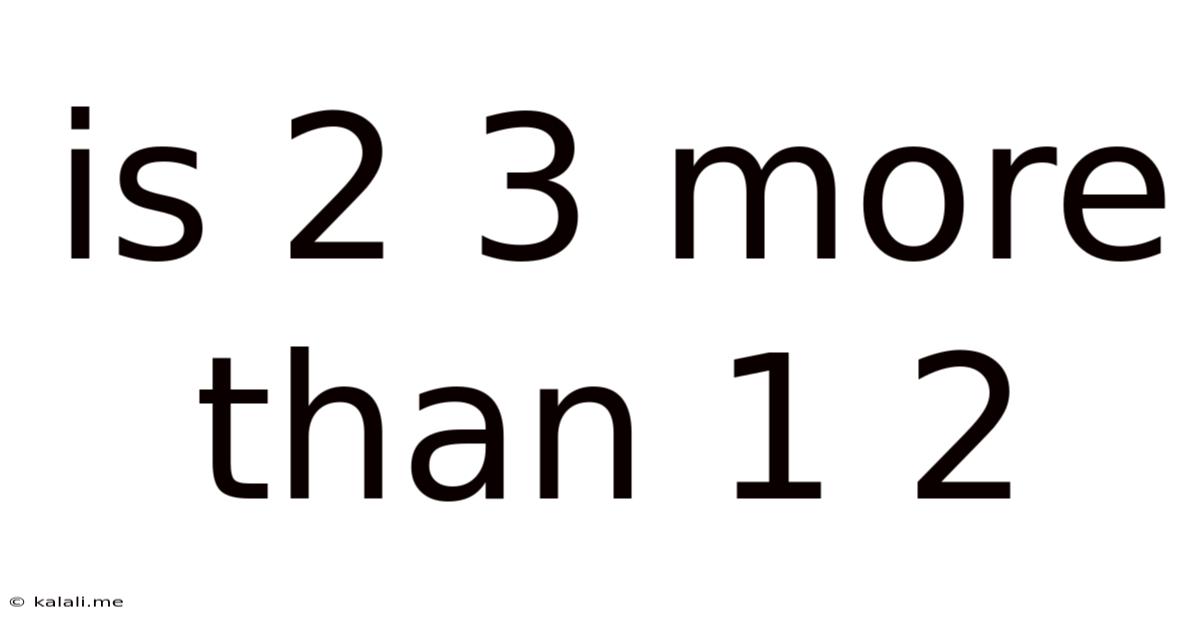
Table of Contents
Is 2/3 More Than 1/2? A Deep Dive into Fraction Comparison
This article will thoroughly explore the question: "Is 2/3 more than 1/2?" We'll delve beyond a simple yes or no answer, providing multiple methods to compare fractions, explain the underlying mathematical principles, and explore practical applications where understanding fraction comparison is crucial. This in-depth analysis will equip you with the knowledge to confidently tackle similar comparisons and improve your understanding of fractions.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator is 2 and the denominator is 3. This means we have 2 out of 3 equal parts.
Method 1: Finding a Common Denominator
This is the most common and reliable method for comparing fractions. The core principle is to rewrite both fractions with the same denominator. This allows for a direct comparison of their numerators.
To find a common denominator for 2/3 and 1/2, we look for the least common multiple (LCM) of 3 and 2. The LCM of 3 and 2 is 6.
-
Converting 2/3: To get a denominator of 6, we multiply both the numerator and the denominator by 2: (2 x 2) / (3 x 2) = 4/6
-
Converting 1/2: To get a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
Now we can compare: 4/6 and 3/6. Since 4 > 3, we conclude that 2/3 > 1/2.
Method 2: Converting to Decimals
Another effective method is converting fractions to decimals. This provides a numerical representation that's often easier to interpret directly.
-
Converting 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667
-
Converting 1/2 to a decimal: 1 ÷ 2 = 0.5
Comparing the decimal values, 0.6667 > 0.5, confirming that 2/3 > 1/2. Note that 2/3 is a recurring decimal, meaning the '6' repeats infinitely. For practical purposes, we use a rounded decimal value.
Method 3: Visual Representation
Visual aids can significantly enhance understanding, especially for beginners. Imagine two identical circles.
-
Representing 1/2: Divide one circle into two equal halves and shade one half.
-
Representing 2/3: Divide the other circle into three equal thirds and shade two thirds.
By visually comparing the shaded areas, it's clear that the shaded area representing 2/3 is larger than the shaded area representing 1/2. This visual confirmation reinforces the conclusion that 2/3 > 1/2.
Method 4: Using a Number Line
A number line provides a graphical representation of numbers, including fractions. Plotting both fractions on a number line clearly shows their relative positions. 2/3 will be positioned to the right of 1/2, indicating that 2/3 > 1/2.
Practical Applications of Fraction Comparison
Understanding fraction comparison is essential in various real-world scenarios:
-
Cooking and Baking: Recipes often require precise measurements using fractions. Comparing fractions ensures you use the correct amounts of ingredients.
-
Construction and Engineering: Accurate measurements and calculations are vital in construction. Comparing fractions is crucial for ensuring precise dimensions and avoiding errors.
-
Finance and Budgeting: Understanding fractions is important for managing personal finances, calculating percentages, and understanding proportions of income and expenses.
-
Data Analysis: Many datasets involve fractions and proportions. Comparing fractions helps in interpreting data and drawing meaningful conclusions.
-
Probability and Statistics: Probability calculations often involve fractions. Comparing fractions is crucial for determining the likelihood of different events.
Beyond the Basics: Comparing More Complex Fractions
The methods described above can be extended to compare more complex fractions. For example, let's compare 5/8 and 3/5.
-
Finding a Common Denominator: The LCM of 8 and 5 is 40.
- 5/8 = (5 x 5) / (8 x 5) = 25/40
- 3/5 = (3 x 8) / (5 x 8) = 24/40
Since 25 > 24, 5/8 > 3/5.
-
Converting to Decimals:
- 5/8 = 0.625
- 3/5 = 0.6
Again, 5/8 > 3/5.
Addressing Potential Misconceptions
A common misconception is focusing solely on the numerators without considering the denominators. Simply stating that 2 is larger than 1 doesn't imply that 2/3 is larger than 1/2. The denominator plays a crucial role in determining the size of the fraction.
Conclusion
The answer to the question "Is 2/3 more than 1/2?" is a resounding yes. This article explored multiple methods – finding a common denominator, converting to decimals, visual representation, and using a number line – to demonstrate this comparison. We also discussed the practical applications of understanding fraction comparison in various fields and addressed potential misconceptions. Mastering fraction comparison is a fundamental skill in mathematics with broad real-world implications. By understanding the underlying principles and applying the techniques outlined here, you can confidently tackle any fraction comparison problem. Remember, the key is to always consider both the numerator and the denominator to accurately determine the relative size of fractions.
Latest Posts
Latest Posts
-
What Does 10ks Mean On A Ring
Jun 30, 2025
-
How Long Is 9 Miles In Minutes
Jun 30, 2025
-
What Is 1 4 Cup Plus 1 4 Cup
Jun 30, 2025
-
How To Pass Level 7 On Bloxorz
Jun 30, 2025
-
What Does Tyh Mean On A Scratch Ticket Massachusetts
Jun 30, 2025
Related Post
Thank you for visiting our website which covers about Is 2 3 More Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.