Is 2 5 Greater Than 1 3
Kalali
Jul 29, 2025 · 5 min read
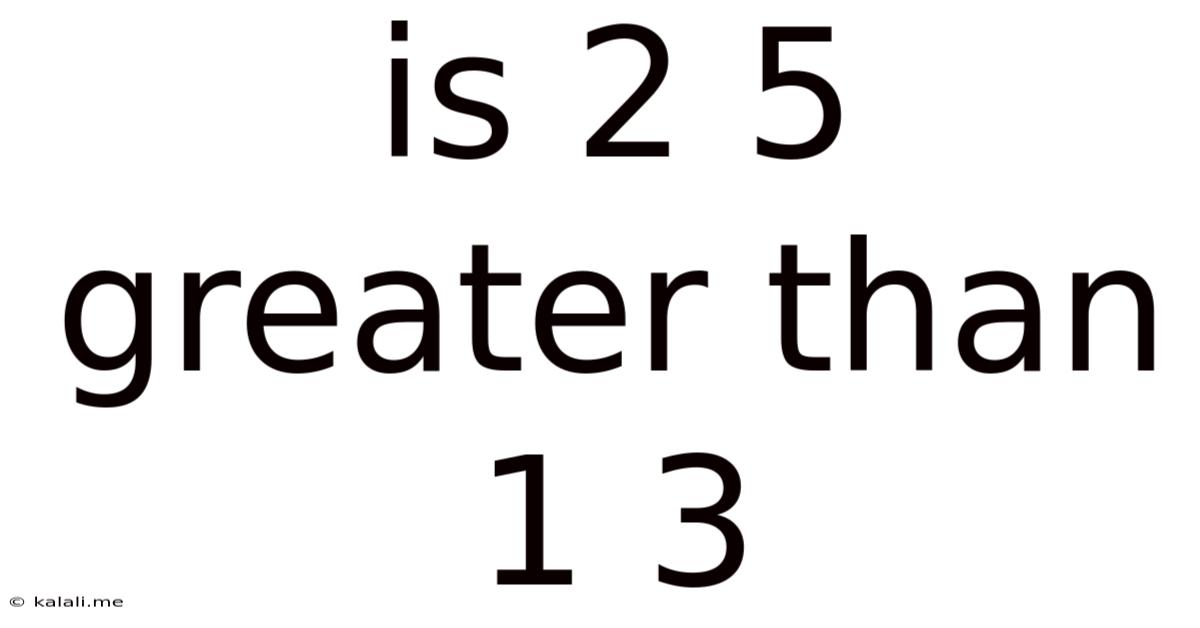
Table of Contents
Is 2/5 Greater Than 1/3? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 2/5 greater than 1/3?", opens the door to a fascinating exploration of fraction comparison techniques, their practical applications, and the underlying mathematical concepts. While the answer itself is straightforward once you understand the methods, the journey to arrive at it reveals crucial skills applicable far beyond simple fraction comparisons. This article will provide a comprehensive guide to comparing fractions, equipping you with various strategies to tackle similar problems with confidence.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's revisit the fundamental concept of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator indicates the total number of equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 2/5, the whole is divided into 5 equal parts, and we're considering 2 of those parts.
Method 1: Finding a Common Denominator
This is perhaps the most widely used and easily understood method. The core principle lies in converting both fractions to equivalent fractions with the same denominator. This allows for a direct comparison of the numerators.
To find a common denominator for 2/5 and 1/3, we need to find the least common multiple (LCM) of 5 and 3. The LCM of 5 and 3 is 15.
-
Converting 2/5: To get a denominator of 15, we multiply both the numerator and denominator by 3: (2 * 3) / (5 * 3) = 6/15
-
Converting 1/3: To get a denominator of 15, we multiply both the numerator and denominator by 5: (1 * 5) / (3 * 5) = 5/15
Now we can easily compare: 6/15 is greater than 5/15. Therefore, 2/5 is greater than 1/3.
Method 2: Converting to Decimals
Another effective method involves converting both fractions into their decimal equivalents. This method is particularly useful when dealing with more complex fractions or when a decimal representation is needed for further calculations.
-
Converting 2/5: To convert 2/5 to a decimal, we divide the numerator (2) by the denominator (5): 2 ÷ 5 = 0.4
-
Converting 1/3: To convert 1/3 to a decimal, we divide the numerator (1) by the denominator (3): 1 ÷ 3 = 0.333... (a repeating decimal)
Comparing the decimals, 0.4 is greater than 0.333..., confirming that 2/5 is greater than 1/3.
Method 3: Visual Representation
For a more intuitive understanding, especially for beginners, visual aids can be extremely helpful. Imagine two identical pies.
-
For 2/5: Divide one pie into 5 equal slices and shade 2 of them.
-
For 1/3: Divide the other pie into 3 equal slices and shade 1 of them.
By visually comparing the shaded portions, it's evident that the shaded area representing 2/5 is larger than the shaded area representing 1/3. This visual confirmation reinforces the conclusion that 2/5 is greater than 1/3.
Beyond the Basics: Expanding the Scope of Fraction Comparison
While the question "Is 2/5 greater than 1/3?" provides a simple starting point, the techniques learned can be applied to more complex scenarios involving:
-
Improper Fractions: Fractions where the numerator is greater than or equal to the denominator (e.g., 7/4). The same methods—finding a common denominator or converting to decimals—apply.
-
Mixed Numbers: Numbers combining a whole number and a fraction (e.g., 2 1/2). Convert mixed numbers to improper fractions before applying the comparison methods. For example, 2 1/2 becomes 5/2.
-
Comparing Multiple Fractions: When comparing more than two fractions, the common denominator method remains the most efficient. Find the LCM of all the denominators and convert all fractions accordingly before comparison.
Real-World Applications of Fraction Comparison
The ability to compare fractions is a crucial skill with numerous real-world applications:
-
Cooking and Baking: Following recipes often requires understanding fraction measurements (e.g., 1/2 cup, 2/3 cup). Comparing fractions helps determine which quantity is larger or smaller.
-
Construction and Engineering: Precise measurements are essential in these fields. Fraction comparison is vital for ensuring accuracy and precision in various tasks.
-
Finance and Budgeting: Understanding fractions is crucial for managing finances, calculating percentages, and comparing proportions of income and expenses.
-
Data Analysis: In various data analysis tasks, comparing fractions helps in understanding proportions, ratios, and trends within datasets.
Advanced Techniques and Considerations
For more advanced scenarios, or when dealing with a large number of fractions, consider these techniques:
-
Cross-Multiplication: This method is particularly useful when comparing two fractions. Cross-multiply the numerators and denominators. The fraction with the larger product in the numerator is the larger fraction. For example, comparing 2/5 and 1/3: (2 * 3) = 6 and (1 * 5) = 5. Since 6 > 5, 2/5 > 1/3.
-
Using a Calculator: Calculators can quickly convert fractions to decimals, facilitating comparison. However, understanding the underlying mathematical principles remains essential.
-
Number Line Representation: Visualizing fractions on a number line provides a clear representation of their relative magnitudes.
Conclusion:
The question, "Is 2/5 greater than 1/3?", serves as a gateway to understanding a fundamental mathematical skill—comparing fractions. This article has explored multiple methods for achieving this, from finding a common denominator to using decimal conversions and visual representations. Mastering these techniques not only answers the initial question but equips you with the tools to confidently tackle various fraction comparison problems in diverse real-world contexts. The ability to effectively compare fractions is a cornerstone of mathematical literacy, opening doors to a deeper understanding of numbers and their applications in numerous fields. Remember, practice is key to mastering any mathematical concept, so try comparing different fractions using the methods discussed above to solidify your understanding.
Latest Posts
Latest Posts
-
How Long Does It Take To Walk 4 Mi
Jul 30, 2025
-
How Old Is Cherry Valance In The Outsiders
Jul 30, 2025
-
How Many Cups Is A Pound Of Lentils
Jul 30, 2025
-
How Much Is 1 Cup Of Cooked Rice In Grams
Jul 30, 2025
-
How Much Was A Gallon Of Milk In 1984
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about Is 2 5 Greater Than 1 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.