Is 3 8 Bigger Than 5 8
Kalali
Jul 27, 2025 · 6 min read
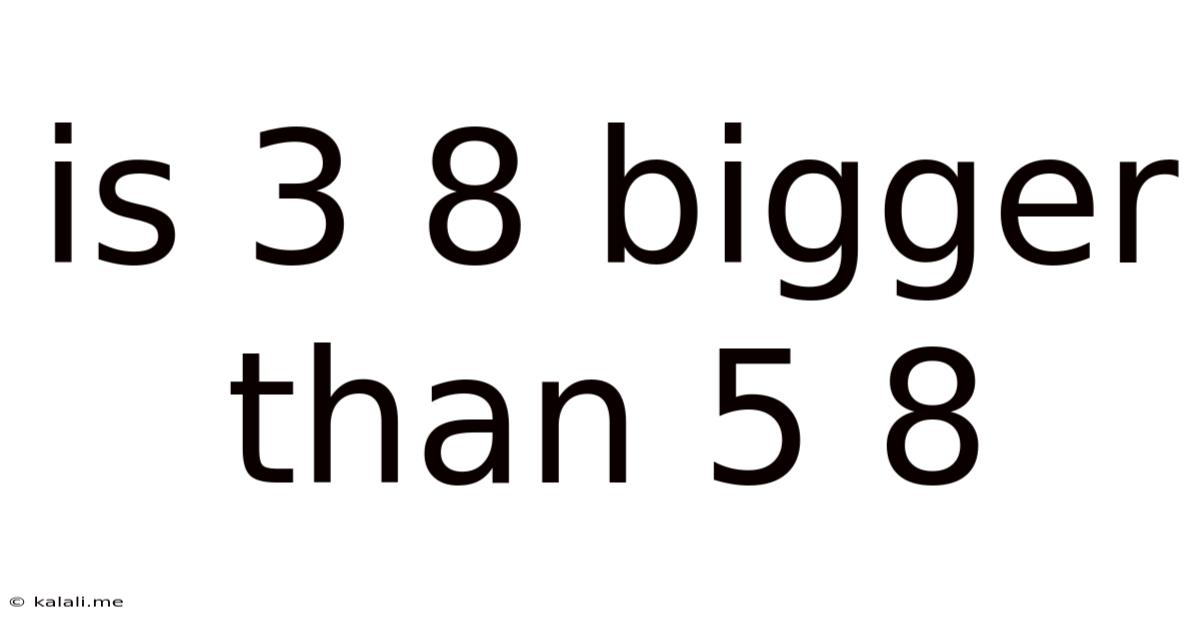
Table of Contents
Is 3/8 Bigger Than 5/8? Understanding Fractions and Comparisons
This seemingly simple question, "Is 3/8 bigger than 5/8?", opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer is immediately apparent to those familiar with fractions, exploring this question allows us to delve into the underlying principles and develop strategies for comparing fractions effectively. This article will not only answer the question definitively but also provide a comprehensive guide to understanding and comparing fractions, equipping you with the skills to tackle more complex fractional comparisons.
Meta Description: Learn how to compare fractions effectively! This comprehensive guide explains whether 3/8 is bigger than 5/8, and provides techniques for comparing any two fractions, including visual aids and step-by-step examples. Master fractions and boost your math skills.
Understanding Fractions: Numerator and Denominator
Before we dive into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number represents the number of parts we have.
- Denominator: The bottom number indicates the total number of equal parts the whole is divided into.
In the fractions 3/8 and 5/8, the denominator, 8, tells us that the whole is divided into eight equal parts. The numerators, 3 and 5, represent the number of those eight parts we're considering.
Visualizing the Comparison: The Power of Representation
One of the most effective ways to understand fraction comparisons is through visualization. Imagine a pizza cut into eight equal slices.
- 3/8: Represents three out of the eight pizza slices.
- 5/8: Represents five out of the eight pizza slices.
By visualizing this, it becomes immediately clear that 5/8 (five slices) is larger than 3/8 (three slices). This visual representation provides an intuitive understanding of the comparison, solidifying the concept.
Direct Comparison: Same Denominator, Easy Comparison
The easiest way to compare fractions is when they share the same denominator, as in our example. When the denominators are identical, we only need to compare the numerators. The fraction with the larger numerator represents the larger portion of the whole.
Since 5 > 3, it follows that 5/8 > 3/8. Therefore, 5/8 is bigger than 3/8.
Comparing Fractions with Different Denominators: Finding a Common Denominator
Comparing fractions with different denominators requires a slightly more involved approach. We need to find a common denominator – a number that is a multiple of both denominators. Let's consider an example: Compare 2/3 and 3/5.
-
Find the Least Common Multiple (LCM): The LCM is the smallest number that is a multiple of both denominators (3 and 5). The LCM of 3 and 5 is 15.
-
Convert to Equivalent Fractions: We convert each fraction to an equivalent fraction with a denominator of 15.
- For 2/3: To get a denominator of 15, we multiply both the numerator and denominator by 5 (15/3 = 5). This gives us 10/15.
- For 3/5: To get a denominator of 15, we multiply both the numerator and denominator by 3 (15/5 = 3). This gives us 9/15.
-
Compare the Numerators: Now that both fractions have the same denominator, we compare the numerators: 10 > 9.
-
Conclusion: Therefore, 10/15 (which is equivalent to 2/3) is bigger than 9/15 (which is equivalent to 3/5).
Cross-Multiplication Method: A Shortcut for Comparison
The cross-multiplication method provides a quick way to compare fractions without finding a common denominator. Let's use the same example, 2/3 and 3/5:
-
Cross-multiply: Multiply the numerator of the first fraction by the denominator of the second fraction (2 x 5 = 10). Then, multiply the numerator of the second fraction by the denominator of the first fraction (3 x 3 = 9).
-
Compare the Products: Compare the two products: 10 > 9.
-
Conclusion: The fraction whose numerator produced the larger product is the larger fraction. Therefore, 2/3 is bigger than 3/5.
Decimal Conversion: Another Approach to Comparison
Converting fractions to decimals offers another method for comparison. This approach is particularly helpful when dealing with more complex fractions or when you need a numerical representation for other calculations.
To convert a fraction to a decimal, simply divide the numerator by the denominator.
- 3/8 = 0.375
- 5/8 = 0.625
Comparing the decimal values, it's evident that 0.625 > 0.375, confirming that 5/8 is larger than 3/8.
Using a Number Line: A Visual Aid for Fraction Comparison
A number line provides a visual representation that aids in comparing fractions. Mark the points 0 and 1 on the number line. Then divide the space between 0 and 1 into equal parts based on the denominators of the fractions you're comparing. Plot the fractions on the number line. The fraction further to the right on the number line is the larger fraction.
Practical Applications of Fraction Comparison
Understanding fraction comparison isn't just an academic exercise; it has numerous practical applications in everyday life:
- Cooking and Baking: Following recipes often requires understanding and comparing fractions (e.g., 1/2 cup vs. 3/4 cup).
- Measurement: Many measurements involve fractions (e.g., inches, centimeters).
- Finance: Calculating portions of budgets or understanding interest rates involves working with fractions.
- Construction and Engineering: Precise measurements and calculations in construction and engineering heavily rely on fractions.
Advanced Fraction Comparison: Dealing with Mixed Numbers
Mixed numbers combine a whole number and a fraction (e.g., 2 1/2). To compare mixed numbers, you can:
- Convert to Improper Fractions: Convert both mixed numbers into improper fractions (a fraction where the numerator is larger than the denominator). Then, use any of the methods previously discussed to compare them.
- Compare the Whole Numbers First: If the whole numbers are different, the mixed number with the larger whole number is the larger number. If the whole numbers are the same, compare the fractional parts using the methods described above.
Troubleshooting Common Mistakes in Fraction Comparison
- Ignoring the Denominator: A common mistake is focusing solely on the numerators when comparing fractions with different denominators. Remember, the denominator plays a crucial role in determining the size of the fraction.
- Incorrect Conversion to Common Denominator: Ensure you correctly multiply both the numerator and the denominator when converting fractions to a common denominator.
- Misunderstanding Cross-Multiplication: Remember that the larger product indicates the larger fraction in the cross-multiplication method.
Conclusion: Mastering Fraction Comparison
The seemingly simple question, "Is 3/8 bigger than 5/8?" has served as a springboard for a thorough exploration of fraction comparison techniques. Understanding fractions and the various methods for comparing them is crucial for success in mathematics and its countless real-world applications. By mastering these techniques, you'll gain confidence in tackling more complex mathematical problems and enhance your problem-solving skills. Remember to choose the method that best suits the fractions you're comparing, and always double-check your work to avoid common errors. With practice and consistent application, comparing fractions will become second nature.
Latest Posts
Latest Posts
-
Has A Hummingbird Ever Killed A Human
Jul 27, 2025
-
How To Say Love You In Hawaiian
Jul 27, 2025
-
How Long Would It Take To Walk 1 5 Miles
Jul 27, 2025
-
How Many Boxes Of Siding In A Square
Jul 27, 2025
-
How Many Cups Is 10 Oz Of Mini Marshmallows
Jul 27, 2025
Related Post
Thank you for visiting our website which covers about Is 3 8 Bigger Than 5 8 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.