Is 3 8 Larger Than 1 2
Kalali
Jul 05, 2025 · 5 min read
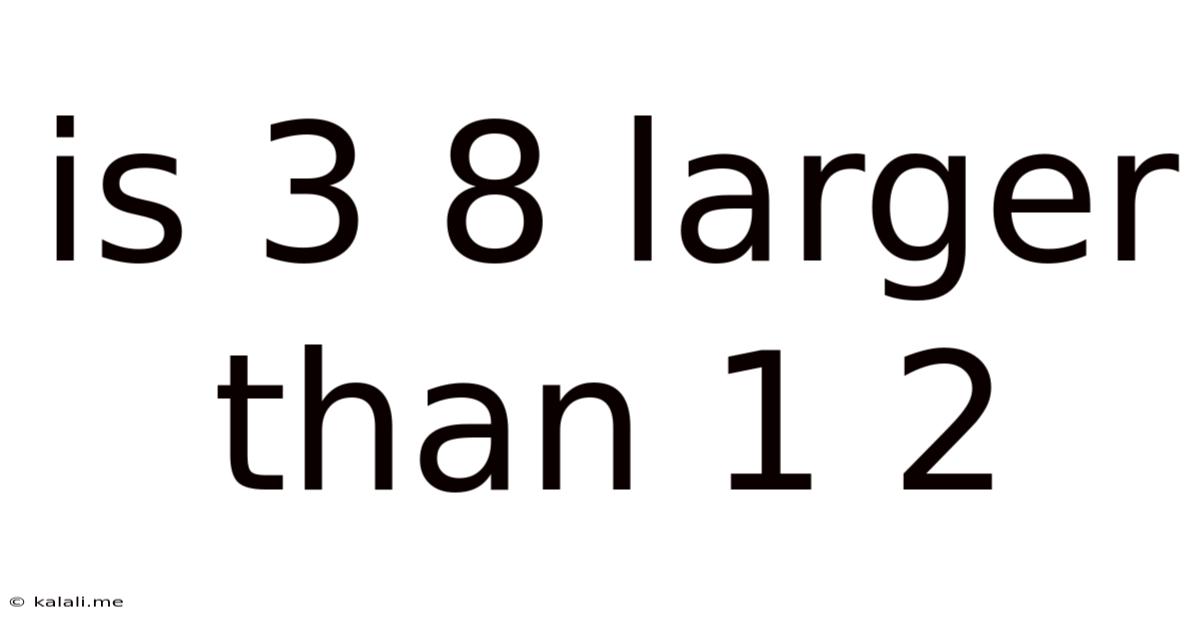
Table of Contents
Is 3/8 Larger Than 1/2? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 3/8 larger than 1/2?", opens the door to a broader understanding of fractions, a fundamental concept in mathematics crucial for various applications from everyday life to advanced scientific calculations. This article will not only answer the question definitively but also explore various methods for comparing fractions, providing you with the tools and knowledge to tackle similar comparisons with ease. Understanding fraction comparison is vital for anyone looking to improve their mathematical skills and problem-solving abilities.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's quickly review the basics of fractions. A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 3/8, 3 is the numerator and 8 is the denominator. This means we have 3 out of 8 equal parts of a whole.
Method 1: Converting to Decimal Equivalents
One of the simplest ways to compare fractions is to convert them into decimal equivalents. This involves dividing the numerator by the denominator.
- 1/2: 1 ÷ 2 = 0.5
- 3/8: 3 ÷ 8 = 0.375
By comparing the decimal equivalents, it's clear that 0.5 (1/2) is larger than 0.375 (3/8). Therefore, 3/8 is not larger than 1/2.
Method 2: Finding a Common Denominator
Another effective method is to find a common denominator for both fractions. A common denominator is a number that is a multiple of both denominators. In this case, the denominators are 2 and 8. The least common multiple (LCM) of 2 and 8 is 8.
- 1/2: To convert 1/2 to a fraction with a denominator of 8, we multiply both the numerator and the denominator by 4: (1 x 4) / (2 x 4) = 4/8
- 3/8: This fraction already has a denominator of 8.
Now, we can easily compare 4/8 and 3/8. Since 4/8 > 3/8, we conclude that 1/2 is larger than 3/8, and therefore, 3/8 is not larger than 1/2.
Method 3: Visual Representation
Visualizing fractions can be particularly helpful, especially for beginners. Imagine a circle divided into equal parts.
- 1/2: Divide a circle into two equal halves. Shading one half visually represents 1/2.
- 3/8: Divide a circle into eight equal parts. Shading three of those parts represents 3/8.
By comparing the shaded areas, it's evident that the area representing 1/2 is larger than the area representing 3/8. This visual confirmation reinforces the conclusion that 3/8 is smaller than 1/2.
Method 4: Cross-Multiplication
Cross-multiplication offers a more algebraic approach. This method involves multiplying the numerator of one fraction by the denominator of the other and vice versa. Compare the resulting products.
- Multiply the numerator of 3/8 (3) by the denominator of 1/2 (2): 3 x 2 = 6
- Multiply the numerator of 1/2 (1) by the denominator of 3/8 (8): 1 x 8 = 8
Since 6 < 8, we can conclude that 3/8 < 1/2. Therefore, 3/8 is not larger than 1/2.
Beyond the Basic Comparison: Exploring Fraction Concepts
The comparison of 3/8 and 1/2 provides a foundation for understanding more complex fraction concepts. Let's explore some related ideas:
Equivalent Fractions:
Equivalent fractions represent the same value despite having different numerators and denominators. For instance, 1/2, 2/4, 4/8, and 8/16 are all equivalent fractions. Understanding equivalent fractions is crucial for finding common denominators and simplifying fractions.
Simplifying Fractions:
Simplifying a fraction involves reducing it to its lowest terms. This is done by dividing both the numerator and the denominator by their greatest common divisor (GCD). For example, 4/8 can be simplified to 1/2 by dividing both the numerator and the denominator by 4.
Improper Fractions and Mixed Numbers:
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 5/4). A mixed number combines a whole number and a proper fraction (e.g., 1 1/4). Converting between improper fractions and mixed numbers is a valuable skill in fraction arithmetic.
Adding, Subtracting, Multiplying, and Dividing Fractions:
Performing arithmetic operations on fractions requires a solid understanding of the fundamental concepts discussed above. Different rules apply to each operation, and mastering them is essential for solving more complex problems. For instance, adding or subtracting fractions requires a common denominator, while multiplying fractions involves multiplying the numerators and denominators separately.
Real-World Applications of Fraction Comparison
The ability to compare fractions is not just a theoretical exercise; it has numerous practical applications in everyday life:
- Cooking and Baking: Following recipes often requires understanding fractions for measuring ingredients accurately.
- Construction and Engineering: Precise measurements are critical in these fields, and fractions play a vital role in ensuring accuracy.
- Finance: Calculating percentages, interest rates, and proportions involves working with fractions.
- Data Analysis: Representing and interpreting data often involves using fractions and percentages.
Conclusion: Mastering Fractions for a Brighter Future
The seemingly simple question, "Is 3/8 larger than 1/2?" has led us on a journey exploring the multifaceted world of fractions. We've examined several methods for comparing fractions – converting to decimals, finding common denominators, visual representation, and cross-multiplication. This exploration highlights the importance of a strong foundation in fractions for success in various mathematical and real-world applications. By understanding these concepts and employing the methods described above, you'll be well-equipped to confidently tackle fraction comparisons and other fraction-related problems, paving the way for further mathematical exploration and achievement. Remember, practice is key; the more you work with fractions, the more comfortable and proficient you'll become.
Latest Posts
Latest Posts
-
Kenmore Series 700 Washer Cubic Square Meters
Jul 30, 2025
-
What Does S And M Mean In The Song
Jul 30, 2025
-
What Is The Melting Point Of Ice
Jul 30, 2025
-
What Is A 16 Out Of 23
Jul 30, 2025
-
El Burro Sabe Mas Que Maduro Translate To English
Jul 30, 2025
Related Post
Thank you for visiting our website which covers about Is 3 8 Larger Than 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.