Is 4 5 Greater Than 2 3
Kalali
Aug 23, 2025 · 5 min read
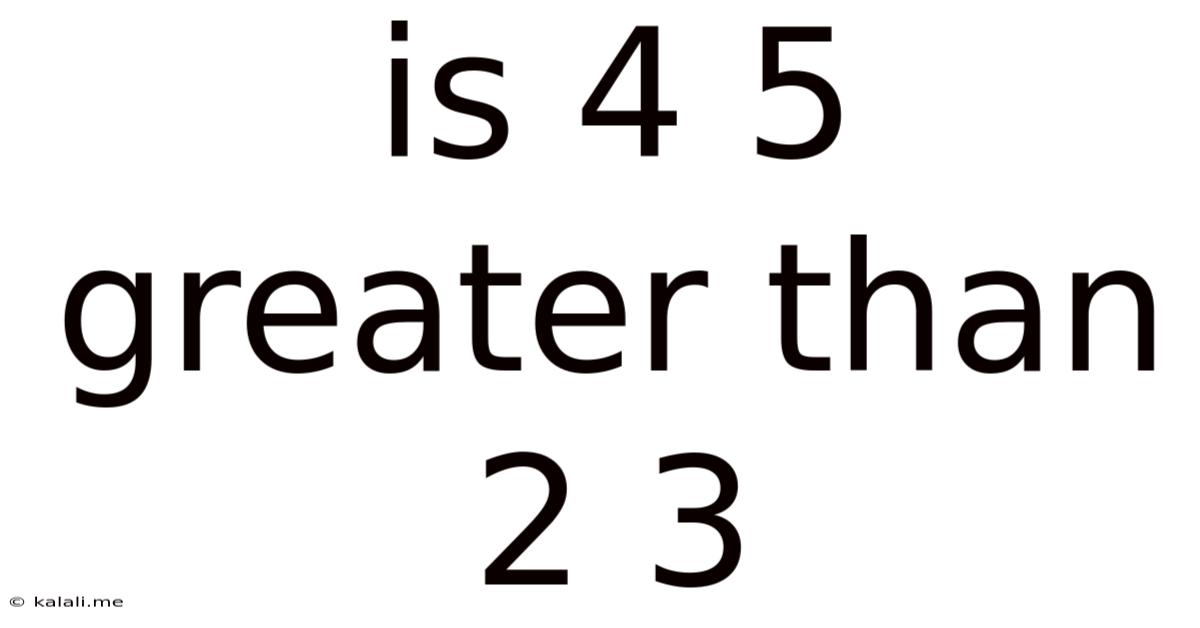
Table of Contents
Is 4/5 Greater Than 2/3? A Deep Dive into Fraction Comparison
This seemingly simple question, "Is 4/5 greater than 2/3?", opens the door to a deeper understanding of fractions, a fundamental concept in mathematics. While the answer might seem obvious to some, exploring the different methods to compare fractions reveals valuable insights into mathematical reasoning and problem-solving strategies. This article will not only answer the question definitively but also equip you with multiple approaches to compare fractions, ensuring you can tackle similar problems with confidence. This is crucial for anyone from elementary school students mastering basic arithmetic to advanced learners tackling more complex mathematical concepts.
Understanding Fractions: A Quick Refresher
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two key components:
- Numerator: The top number, indicating the number of parts we have.
- Denominator: The bottom number, indicating the total number of equal parts the whole is divided into.
For example, in the fraction 4/5, the numerator (4) tells us we have 4 parts, and the denominator (5) tells us the whole is divided into 5 equal parts.
Method 1: Finding a Common Denominator
This is arguably the most common and straightforward method for comparing fractions. The core principle is to rewrite both fractions with the same denominator. This allows for a direct comparison of the numerators. To find a common denominator, we find the least common multiple (LCM) of the denominators.
Let's apply this method to compare 4/5 and 2/3:
-
Find the LCM of 5 and 3: The LCM of 5 and 3 is 15 (since 5 x 3 = 15 and there are no smaller common multiples).
-
Rewrite the fractions:
- To change 4/5 to a fraction with a denominator of 15, we multiply both the numerator and the denominator by 3: (4 x 3) / (5 x 3) = 12/15
- To change 2/3 to a fraction with a denominator of 15, we multiply both the numerator and the denominator by 5: (2 x 5) / (3 x 5) = 10/15
-
Compare the numerators: Now that both fractions have the same denominator, we simply compare the numerators: 12 > 10.
-
Conclusion: Therefore, 12/15 (or 4/5) is greater than 10/15 (or 2/3).
Method 2: Converting Fractions to Decimals
Another effective method involves converting fractions into decimals. This approach is particularly helpful when dealing with fractions that are difficult to compare using a common denominator. The process involves dividing the numerator by the denominator.
Let's apply this method to compare 4/5 and 2/3:
-
Convert 4/5 to a decimal: 4 ÷ 5 = 0.8
-
Convert 2/3 to a decimal: 2 ÷ 3 ≈ 0.6667 (this is a recurring decimal)
-
Compare the decimals: 0.8 > 0.6667
-
Conclusion: Therefore, 4/5 is greater than 2/3.
Method 3: Visual Representation (using diagrams)
Visual aids can be incredibly helpful, especially when teaching fractions to younger learners. Representing each fraction using a diagram allows for a direct visual comparison.
Imagine two identical circles:
- For 4/5: Divide the first circle into 5 equal slices. Shade 4 of them.
- For 2/3: Divide the second circle into 3 equal slices. Shade 2 of them.
By visually comparing the shaded areas, it's clear that the shaded portion in the 4/5 circle is larger than the shaded portion in the 2/3 circle.
Method 4: Cross-Multiplication
This method provides a shortcut for comparing two fractions without finding a common denominator. It involves multiplying the numerator of one fraction by the denominator of the other and vice versa.
-
Cross-multiply:
- Multiply the numerator of 4/5 (which is 4) by the denominator of 2/3 (which is 3): 4 x 3 = 12
- Multiply the numerator of 2/3 (which is 2) by the denominator of 4/5 (which is 5): 2 x 5 = 10
-
Compare the products: 12 > 10
-
Conclusion: Since 12 is greater than 10, 4/5 is greater than 2/3. The larger product corresponds to the larger fraction.
Method 5: Comparing to Benchmarks (1/2)
Sometimes, comparing fractions to a benchmark like 1/2 can simplify the process. This method is useful for quick estimations.
- 4/5: 4/5 is clearly greater than 1/2 because 4 is more than half of 5.
- 2/3: 2/3 is also greater than 1/2 because 2 is more than half of 3.
However, this method alone doesn't definitively show which fraction is larger. It's best used in conjunction with other methods for a precise comparison.
Addressing Potential Misconceptions
When comparing fractions, some common misconceptions can arise:
- Focusing solely on numerators: Simply comparing numerators without considering the denominators is incorrect. While a larger numerator might suggest a larger fraction, the denominator plays a crucial role in determining the size of the fraction.
- Incorrectly applying cross-multiplication: Remember to compare the resulting products from cross-multiplication correctly. The larger product corresponds to the larger fraction.
- Ignoring equivalent fractions: Understanding equivalent fractions is crucial. A fraction can be represented in multiple ways (e.g., 1/2 is equivalent to 2/4, 3/6, etc.).
Practical Applications and Real-World Examples
The ability to compare fractions is essential in various real-world scenarios:
- Baking: Following recipes often requires understanding and comparing fractions of ingredients.
- Construction: Measuring materials and following blueprints often involves working with fractions.
- Finance: Calculating percentages and proportions in financial matters necessitates a strong understanding of fractions.
- Data Analysis: Interpreting data represented in fractional form is crucial in numerous fields.
Conclusion: Mastering Fraction Comparison
This in-depth exploration has provided a comprehensive answer to the question, "Is 4/5 greater than 2/3?" The answer is a resounding yes. Furthermore, we've explored multiple methods for comparing fractions, highlighting their strengths and weaknesses. Mastering these techniques is not only crucial for academic success in mathematics but also incredibly valuable for navigating numerous real-world situations that involve fractions and proportions. By understanding the underlying principles and employing appropriate methods, you can confidently compare any two fractions and accurately determine their relative sizes. Remember to choose the method most comfortable and efficient for you, depending on the complexity of the fractions involved.
Latest Posts
Latest Posts
-
How Far Is Destin Florida From Tallahassee Florida
Aug 23, 2025
-
How Old Are You Born In 1977
Aug 23, 2025
-
Weight Of 2 Cu Ft Of Soil
Aug 23, 2025
-
To Kill A Mockingbird How Many Pages
Aug 23, 2025
-
Forty Six Thousand And Fifty Eight As A Number
Aug 23, 2025
Related Post
Thank you for visiting our website which covers about Is 4 5 Greater Than 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.